Insectoid Curve

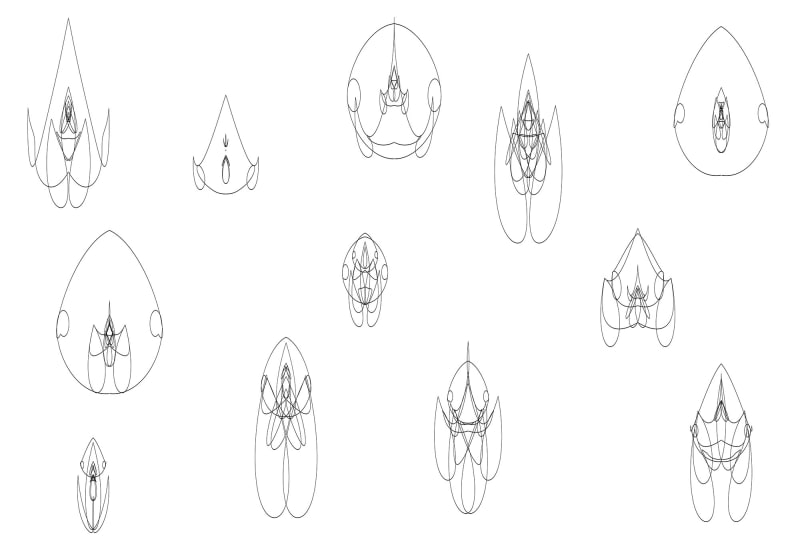
The following short article will discuss the Insectoid Curve - a parametric curve inspired by the Scarabaeus and Cornoid. I created this back in 2016 for fun.

The curve itself is a weighted average of variations on both the Cornoid and the Scarabaeus. The equation is parametric, with $\theta$ as the parameter in a range from $0$ to $2\pi$ .

$$r = b \cos(2 \theta) - a \cos(\theta) \newline x_1 = 2|r \cos(\theta + \pi/2)| \newline y_1 = \text{atan}( r \sin(\theta 2)) \newline x_2 = c \cos(\theta) (1 - (2 \sin^2(\theta)) \newline y_2 = c \sin(\theta) (1 + (2 \cos^2(\theta)) \newline x = x_1 d + x_2 e \newline y = y_1 d + y_2 e$$

Values $a,b,c,d$ and $e$ all range from $0$ to $1$ . In the below image these values were simply randomized:

Note each of the above plots is actually the result of $4$ randomly generated plots on top of one another and increasingly offset on the $y$ axis (slightly).

Interactive Version

Click the below plot - values $a$ through $e$ will be randomized.

The code here is a bit strange, something I speedcoded to quickly create responsive shapes/plots. I may revisit it some day, but for now it remains a bit of an esolang api.

Again, this is $4$ plots on top of one another. To render this plot with a single layer hold your shift key and click.

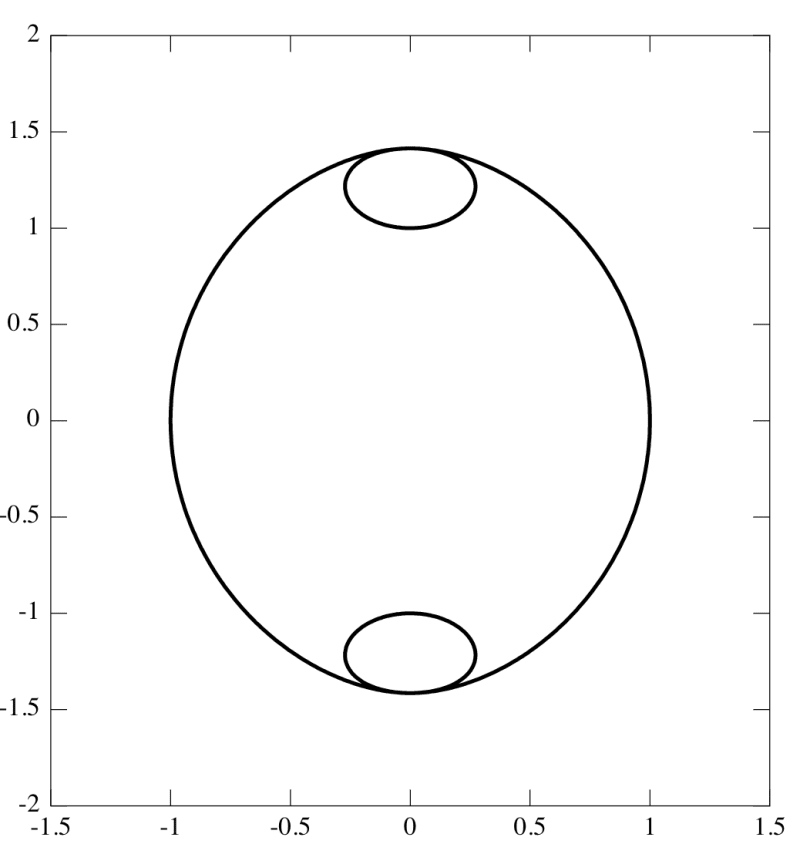
The Scarabaeus and Cornoid

The original equation for the Scarabaeus curve in polar coordinates is:

$$r = b \cos(2 \theta) - a \cos(\theta)$$

...and the Cornoid in parametric form:

$$x = a \cos (\theta) (1 - 2 \sin^2(\theta)) \newline y = a \sin (\theta) (1 + 2 \cos^2(\theta))$$

Quick Background

The original impetus for the creation of the Insectoid Curve was to create a curve that had features similar to an insect - specifically a beetle. After combining the Cornoid and Scarabaeus the result you see here is the result.