MULTISTAGE GRAPH

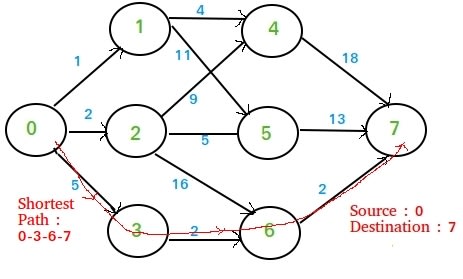
A Multistage graph is a directed graph in which the nodes can be divided into a set of stages such that all edges are from a stage to next stage only (In other words there is no edge between vertices of same stage and from a vertex of current stage to previous stage).

We are give a multistage graph, a source and a destination, we need to find shortest path from source to destination. By convention, we consider source at stage 1 and destination as last stage.

The strategies that can be used are:

• Brute force method
• Dijkstra’s Algorithm
• Simple Greedy Method
• Dynamic Programming

Implementation

// C# program to find shortest distance
// in a multistage graph.
using System;

class GFG
{
    static int N = 8;
    static int INF = int.MaxValue;

    // Returns shortest distance from 0 to
    // N-1.
    public static int shortestDist(int[,] graph) {

        // dist[i] is going to store shortest
        // distance from node i to node N-1.
        int[] dist = new int[N];

        dist[N-1] = 0;

        // Calculating shortest path for
        // rest of the nodes
        for (int i = N-2 ; i >= 0 ; i--)
        {

            // Initialize distance from i to
            // destination (N-1)
            dist[i] = INF;

            // Check all nodes of next stages
            // to find shortest distance from
            // i to N-1.
            for (int j = i ; j < N ; j++)
            {
                // Reject if no edge exists
                if (graph[i,j] == INF)
                    continue;

                // We apply recursive equation to
                // distance to target through j.
                // and compare with minimum distance
                // so far.
                dist[i] = Math.Min(dist[i], graph[i,j] +
                                            dist[j]);
            }
        }

        return dist[0];
    }

    // Driver code
    static void Main()
    {
        // Graph stored in the form of an
        // adjacency Matrix
        int[,] graph = new int[,]
        {{INF, 1, 2, 5, INF, INF, INF, INF},
        {INF, INF, INF, INF, 4, 11, INF, INF},
        {INF, INF, INF, INF, 9, 5, 16, INF},
        {INF, INF, INF, INF, INF, INF, 2, INF},
        {INF, INF, INF, INF, INF, INF, INF, 18},
        {INF, INF, INF, INF, INF, INF, INF, 13},
        {INF, INF, INF, INF, INF, INF, INF, 2}};

        Console.Write(shortestDist(graph));
    }
}

Output

9

Time Complexity
O(n^2)