Intro: About the Caesar Cipher
The Caesar Cipher is a simple cipher that has been around for a long time. Julius Caesar used it in some of his correspondence over 2000 years ago. It has applications in other ciphers, but offers no useful level of security due to how easy it is to decipher.
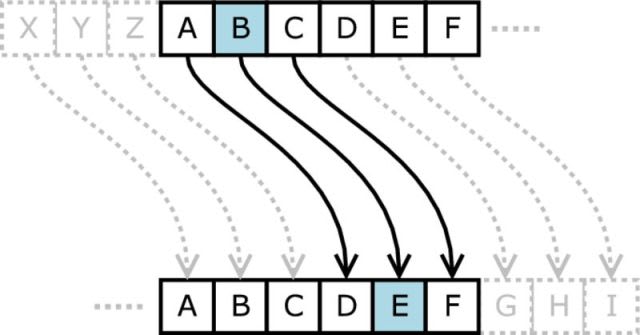
The cipher works by shifting each letter in a message the same amount for each letter. For example, if I set my rotation factor to three, the letter ‘a’ yields ‘d’.
To see this more clearly, the diagram below demonstrates how to handle shifts that reach the end of the alphabet. As the shift reaches the end of the alphabet, the ‘z’ wraps around and becomes ‘c’ using a shift of three.
Now, let’s take a more complete example. If we use a right shift of 20 and and apply it to each letter in the message “Hello World!”, we get the ciphertext “Byffi Qilfx!”
Conversely, if we want to decrypt this, we apply the cipher in reverse and shift left instead of right. From this, we see that the two variable parts of the cipher are 1.which way you shift, and 2. by how much.
Coding the Cipher
As an exercise, I wrote a simple python script to perform the rotations for me. First, I worked out the math for handling the shift (including wrapping) since this was the most complex part. Then, I iterated through each character and applied the computation. Finally, I added a simple CLI and then posted it to Github.
Below is my Caesar cipher implementation. Python doesn’t let you perform math operations on letters so you have to use the “ord” function to convert them to the Unicode code point first.
def apply_rotation(c, factor):
"""Applies a shift of factor to the letter denoted by c"""
if c.isalpha():
lower = ord('A') if c.isupper() else ord('a')
c = chr(lower + ((ord(c) - lower + factor) % 26))
return c
def caesar_cipher(s, k):
"""Iterates through each letter and constructs the cipher text"""
new_message = ''
factor = k % 26
for c in s:
new_message += apply_rotation(c, factor)
return new_message
The Math
Let’s work through the apply_rotation method with a single letter, ‘a’ since this is a little difficult to read.
First, we assign the value of “lower” to ‘A’ or ‘a’ depending on the case to construct the shift. Looking at the inner parentheses we convert the character to a code point and subtract “lower”. The letter ‘a’ has a code point of 97 so if our letter denoted by the variable ‘c’ was ‘f’ (which has a code point of 102) we would get 5 (102 – 97 = 5). We can then add our shift factor (3 for our example) which gives us 8.
Before looking at the rest of the math, if you index the 26 letter alphabet 1-26, 5 is the letter ‘f’ which is what we want to transform. Adding the shift gives us 8 which maps to the letter ‘i’ which is our current result. Python doesn’t know 8 yields and ‘i’ though, but that’s okay because the remaining part of the equation fixes it up for us.
Performing a modulus of 26 just returns 8 for this example so we can ignore that for now. That leaves us with the last step of adding the Unicode code point value of “lower” to 8 i.e. 97 + 8 = 105. Now we can convert the Unicode code point back to a string using the python built-in method “chr” which gives us ‘i’.
Modulus
This is pretty simple math though, so why do we add lower and subtract it in the same equation? Don’t those cancel each other out? Yes, but since the alphabet is based on 26 characters we need to 0 out the Unicode code point values to our 1-26 index so that we can make use of the modulus to handle shifts that need to wrap.
The modulus helps us with our code wrapping. If we go through the math again, but instead apply a shift of 3 to the letter ‘z’ which has a code point of 122 we have to wrap the letters otherwise we get a code point of 125 which is the character ‘}’.
Ignoring the final, addition of “lower” the equation ends up being (122 – 97 + 3) % 26. This reduces down to 28 % 26. 28 isn’t in the alphabet, however when we apply the modulus we end up with 2. We finally can add the last “lower” to finish up with math which is 97+2 = 99. Applying the chr method we get the letter ‘c’.
Bonus: In the full code example, I use modulus 26 to handle shifts greater than 26. e.g. A shift of 27 is the equivalent of 1 (27 % 26 = 1).
Summary
The Caesar cipher is a simple cipher that shifts each letter by a set amount. We produce the deciphered message, by performing the shift in reverse.
The post Caesar Cipher Implementation in Python appeared first on Morgan Adams.



Top comments (0)