Thank you for your solutions! I like your solution to part 1 especially, I implemented it first with brute force but then ended up optimizing it, but I still only got O(n log n) performance with sorting the list and then performing binary search. Your solution is a bit simpler and more elegant 😄
For your question about optimizing by never looking into any combination twice, I think it's still O(n^2) because although in practice we go through less elements, the amount of iterations still increases fast when n increases.
So if we have a list of five numbers we have to iterate 4+3+2+1 elements (10 in total). With 10 elements there are 45 iterations, with 20 there are 190 and so on. With 200 elements it's already 19 900 iterations. This can also be expressed as arithmetic sequence: 1+2+3+4+...+n. I had the intuition that the optimization like that doesn't matter, but I couldn't convince myself at first so I draw two plots with python.
This is a picture of growth without the optimization:
This is a picture of growth with the optimization:
As you can see, the growth is still as fast. I wanted to have some kind of formal proof for that as well, so that's when I googled it and found this stack overflow question and answer: stackoverflow.com/a/44255732 😊
This is of course the case for the part 1 only, I didn't have time to think through how the optimization affects the performance of part 2!
Thanks Anniina for your comment! Great with the visuals and the stack-overflow link. My key take-away is then that the extra keystrokes required to implementing "never check same twice" is not worth haha :)
Haha yeah well in practice it's faster, but the time complexity is still the same.
I just wrote a blog post about different solutions to the puzzle and their time complexities, you can check my sort + binary search solution from the post if you like: dev.to/annisalli/understanding-tim... 😊 The sort + binary sort is still less optimal than your solution with set, but it was fun to implement it!
For further actions, you may consider blocking this person and/or reporting abuse
We're a place where coders share, stay up-to-date and grow their careers.
Thank you for your solutions! I like your solution to part 1 especially, I implemented it first with brute force but then ended up optimizing it, but I still only got O(n log n) performance with sorting the list and then performing binary search. Your solution is a bit simpler and more elegant 😄
For your question about optimizing by never looking into any combination twice, I think it's still
O(n^2)because although in practice we go through less elements, the amount of iterations still increases fast when n increases.So if we have a list of five numbers we have to iterate 4+3+2+1 elements (10 in total). With 10 elements there are 45 iterations, with 20 there are 190 and so on. With 200 elements it's already 19 900 iterations. This can also be expressed as arithmetic sequence: 1+2+3+4+...+n. I had the intuition that the optimization like that doesn't matter, but I couldn't convince myself at first so I draw two plots with python.
This is a picture of growth without the optimization:
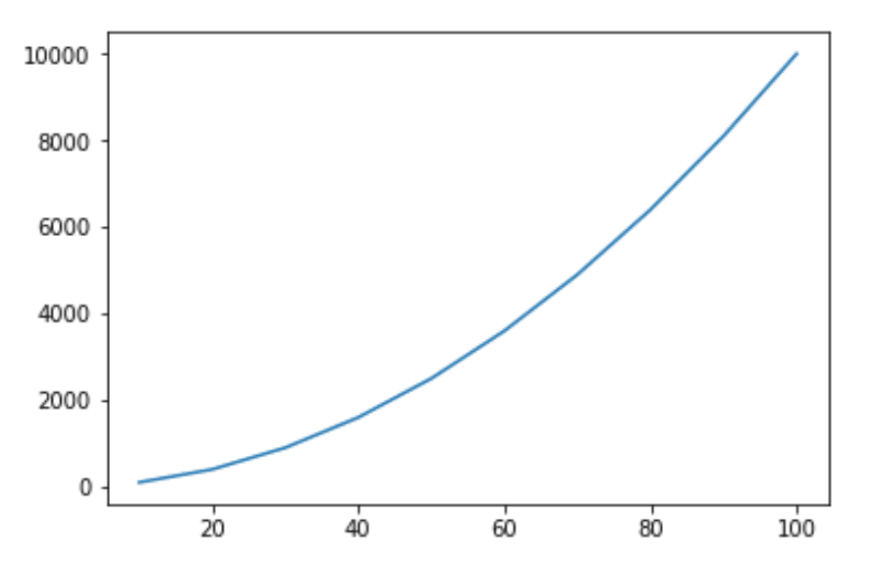
This is a picture of growth with the optimization:
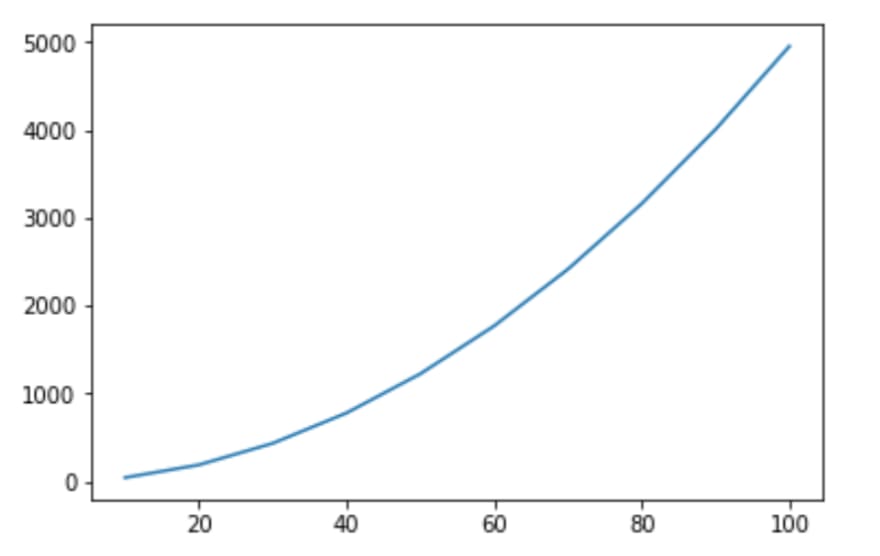
As you can see, the growth is still as fast. I wanted to have some kind of formal proof for that as well, so that's when I googled it and found this stack overflow question and answer: stackoverflow.com/a/44255732 😊
This is of course the case for the part 1 only, I didn't have time to think through how the optimization affects the performance of part 2!
Thanks Anniina for your comment! Great with the visuals and the stack-overflow link. My key take-away is then that the extra keystrokes required to implementing "never check same twice" is not worth haha :)
Oh nice with using sorting and binary search! Seems that python's built-in sort uses timsort which has worst case O(n log(n)). So that would be easy for me to add. How did you solve the binary search part in this puzzle? :)
Haha yeah well in practice it's faster, but the time complexity is still the same.
I just wrote a blog post about different solutions to the puzzle and their time complexities, you can check my sort + binary search solution from the post if you like: dev.to/annisalli/understanding-tim... 😊 The sort + binary sort is still less optimal than your solution with set, but it was fun to implement it!