Maximum Sum Circular Subarray

Given a Circular Sub Array we need to find maximum possible sum

This Problem is an extension of Kadane's Algorithm which is used to find maximum sum in a non Circular Sub Array

Let's consider the following cases

Case 1: All Positive Numbers

arr = [1,2,3,4]

The answer is 10, since the whole array makes upto Maximum sub array

Case 2: All Negative Numbers

arr = [-1,-2,-3,-4]

The answer is the smallest number in the array which is -1

Case 3: Mix of Positive and Negative Numbers

The solution can be at two places

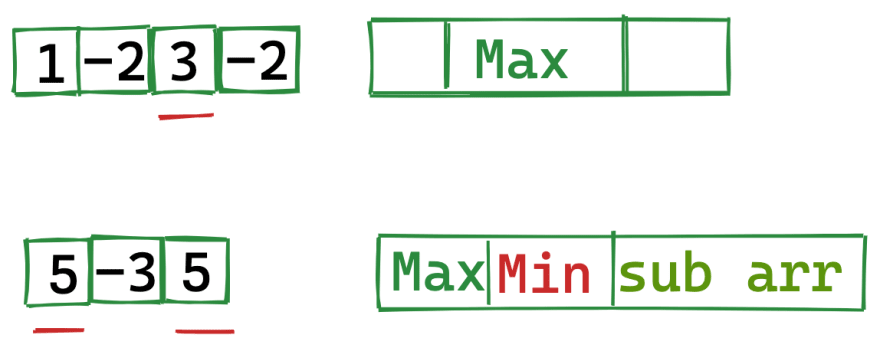
1. [1,-2,3,-2] The answer is 3 which is in the middle
2. [5,-3,5] The answer is 10 which is part of starting sub array and ending sub array

From above image we can solve for the first case (max sum lies in the middle of array) by just applying Kadane's Algorithm

For the second case (max sum lies in the beginning and ending of array):

1. Compute NonCircularMaxSum
2. Find the Total Sum of the Array
3. Here's the tricky part, we change the array to negative array and apply Kadane's algorithm which will now return the min (check above image)
4. Now the max subarray sum for circular is total - min (In the example it's 13 - 3 = 10)
5. If the circular sum is less than or equal to 0 return non circular sum (case for all negative numbers where total sum - min sum equals to 0 [-3,-2,-1])
6. return max of circular sum and non circular sum

Here's the solution

/**
 * @param {number[]} A
 * @return {number}
 */
var maxSubarraySumCircular = function(A) {
    let nonCircularSum = kadaneMaxSum(A)

    let totalSum = 0

    A = A.map(elem => {
        totalSum += elem
        return -elem
    })

    let circularSum = totalSum + kadaneMaxSum(A)

    if(circularSum <= 0) {
        return nonCircularSum
    }

    return Math.max(circularSum, nonCircularSum)
};

let kadaneMaxSum = (arr) => {
    let max = arr[0], cur = arr[0]
    for(let i = 1; i < arr.length; i++) {
        cur = arr[i] + Math.max(cur, 0)
        max = Math.max(max, cur)
    }
    return max
};