Count Square Submatrices with All Ones - Leet Code

Given a m * n matrix of ones and zeros, return how many square submatrices have all ones.

Example 1:

Input: matrix =
[
  [0,1,1,1],
  [1,1,1,1],
  [0,1,1,1]
]
Output: 15
Explanation: 
There are 10 squares of side 1.
There are 4 squares of side 2.
There is  1 square of side 3.
Total number of squares = 10 + 4 + 1 = 15.

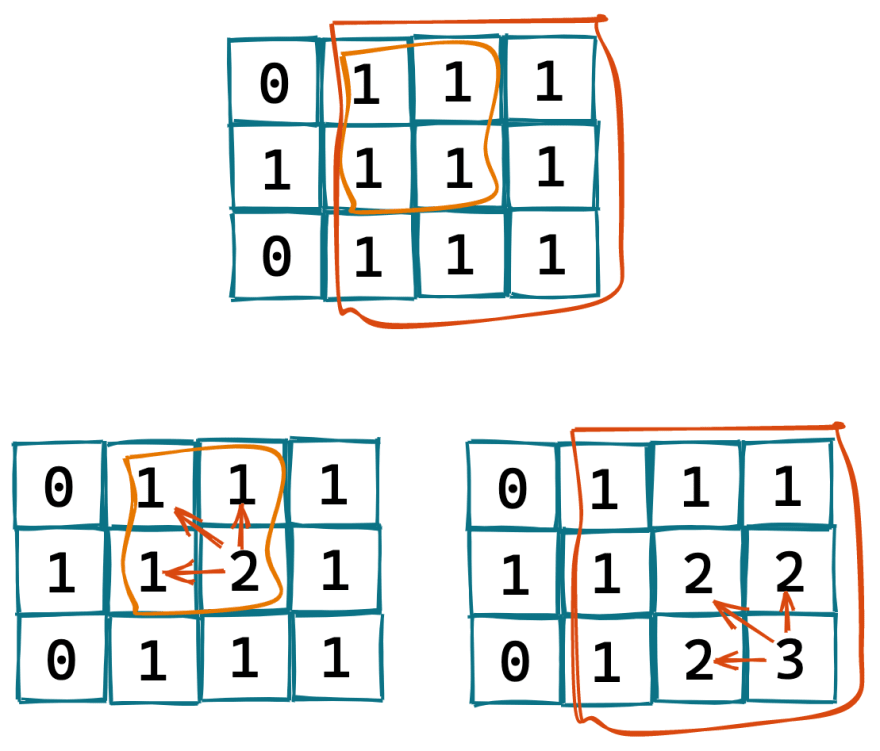
The trick here is to find how many squares can be formed at matrix[i][j]

From the image you can say that

matrix[i][j] = min(matrix[i - 1][j], matrix[i][j - 1], matrix[i - 1][j - 1]) + 1

In words it's the minimum of top, left and diagonal and the current square so add 1

You can solve this by recursion and checking matrix[i][j] can make a square, but it will be O(n^3)

To optimize we can use above technique, which is basically dynamic programming

Algorithm:

1. Initialize a result matrix to add up square matrices as encountered
2. Loop through each element matrix[i][j] and check the maximum square can be formed at that point
3. Add matrix[i][j] to res

Here's the code:

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var countSquares = function(matrix) {
    let res = 0
    for(let i = 0; i < matrix.length; i++) {
        for(let j = 0; j < matrix[0].length; j++) {
            if(matrix[i][j] == 1 && i > 0 && j > 0) {
                matrix[i][j] = Math.min(matrix[i-1][j], matrix[i][j-1], matrix[i-1][j-1]) + 1
            }
            res += matrix[i][j]
        }
    }
    return res
};

Comments

[R. Gurung]

You just told the algorithm instead of talking about the intuition on how to come up with such algorithms, why are you even using minimum value of all but not maximum or diagonal value?

[Ali Ahsan]

what are your observations generally for questions like these? This is so neat