Today I am going to talk about something that I have found comes up with programming all the time, and to this day, even though I can implement it (sometimes). I often find it incredibly difficult to map out in my head and wrap my head around. Recursion. Now I have asked a lot of people why they use recursion and I have never gotten a good answer. It almost as if it is a fancy way of getting a function to work. To talk about recursion we have to understand it on an extremely basic form and then I will attempt to explain it using examples and comparing it to iteration.
Just in case the reader is not aware, iteration is the way that we often solve many problems with programming. Many problems will be based around a list of things or a data set. We might be finding something, replacing something, removing something, adding something, you get the idea. But the point is that there will often be many things that we have to look through or examine in order to get our expected result. Using iteration we wait for it...iterate through a list or a set and when we get to whatever we need we do whatever we need to do.
There are problems with iteration though. Regular iteration requires us to know our boundaries, the beginning and the end of a list/set. This is where recursion can come into play. And this is where I get annoyed sometimes with the answers that I get from people for their reasoning behind using recursive algorithms. When I first learned programming I learned how to iterate through lists or sets first by using a for loop. Then we get to this problem that I just mentioned and the way we get around not knowing our boundaries is by using a while loop.
A while loop will continue running until you either break your machine or you hit what your while loop constraint is. So boom boundary problem solved. But then you learn farther down the programming road about recursion. In simple terms a recursive function is one that calls on itself. So what does that mean? How does that even work? Well, let me do my best to explain. Lets imagine we have a simple function where we want to add all the digits of a big number. So we have something like 54321 and we want to add 5 + 4 + 3 + 2 + 1.
This seems pretty simple right but what if the number was like 124897589379483759843257918471983714. Well you get the idea. The point is there is a way to do this with recursion that is super simple. First what we need is a base case. This is a case where our recursion will end. Then we need our recursive case. This is where we will need to call our function on itself again. Now observe this function :
What this function does, is that it will first check the base case. Is our number 0? No, so we hit the recursive case. Our number % 10 will give us the last digit on the number. Then we add it to our recursive call on our own function which now has our number divided by 10 which will remove that last digit. This will keep calling itself until it is out of numbers in our x.
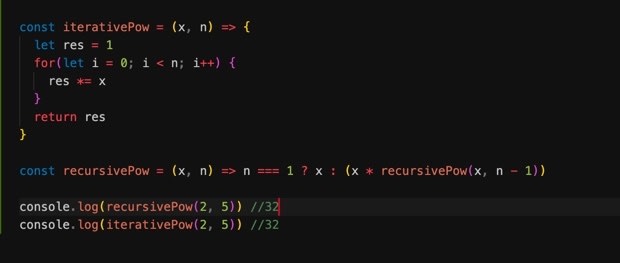
If that didnt make sense this is another example. In this case we want to raise our x to the power of n. We could do this iteratively by making a loop from 1 to n and multiplying our x by itself until the loop runs through, or we can make a recursive function. This function would work very similarly to our plus function except it would do the multiplication. It checks whether or not our number is 1, which will end the recursion, and if its not it will call upon itself and reduce our n by 1 until we are finally at 1 and we are finished.
While these examples of recursion seem pretty basic, I have always found it pretty hard to think of problems in a recursive manner. To this day, I havent heard a solid answer on why one might use recursion. In fact, many places I see online say that many languages would prefer to not use recursion. If you find out(or just already know) a clear reason why, let me know!



Top comments (0)