DEV Community

Chris Rhodes

Posted on Jan 28, 2020

OpenCL - The Wrong Way - Part 2.1

#opencl #parallel

Introduction

In the last post in this series we looked at the general overview of OpenCL and how you could apply a kernel to a list of data. In this post we are going to look how to apply the same idea to a list of integers, and how this approach is the wrong way, and why the data dependencies get in our way. We will then look at reducing the problem further and look at doing some writing of OpenCL.

As a quick meta aside, I have been having a lot of trouble getting these posts out. As I am diving deeper and deeper into OpenCL, parallel algorithms and writing about it, I am finding I can include a lot of information but become crippled when deciding what to include. So for this, and future posts I am going to be reducing the scope of what I talk about until I can write these in a decent amount of time.

As always, the code for this is available on GitHub in the "summing_numbers" folder, note it only deals with the second part of this post as a solution.

crr0004 / adventures-in-opencl

A accompanying repo for my writing about OpenCL

adventures-in-opencl

A accompanying repo for my writing about OpenCL - https://dev.to/crr0004/series/1481

Building

You will need a driver that implements OpenCL 2.0 and cmake.

This was compiled using clang. It should automatically pick up your primary OpenCL vendor and use that.

Headers

The OpenCL headers are included in this repo under shared, if CMake doesn't find them, you can override the directory with "-DOPENCL_INCLUDE_DIRS=../../shared/" when building from one of the build directories. Change the path if it is different for you.

When running it will print out what device is being used but if your vendor implementation is broken it can crash your driver.

Running

Run each sample from the source directory as it needs to pick up the kernel files

Used libraries

Catch2 https://github.com/catchorg/Catch2
Google Benchmark https://github.com/google/benchmark/

See LICENSE file for addition of respective licenses

View on GitHub

Problem Statement

As with all problem solving, start with your problem statement.

Ours is, given a list of integers, for each integer, sum all previous integers to the current one.

For those who have seen this before, it is quite a common task when looking at generation problems involved in weighting. This is a sub-problem of the painters partition problem when using dynamic programming to solve it. In a following post we will be solving the painters partition problem using a parallel solution.

Solution

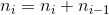
Due to the nature of transitive properties of adding numbers, that is, all previous properties apply to the current, we can transform this problem to simply adding the previous number to the current one. The formula as follows $n_i=\\sum_{k=0}^{i}n_k$ becomes $n_i=n_i+n_{i-1}$ where i is the index of each number in the list. This just means that if we keep running a sum of all the numbers so far, we don't have to add the entire set each time.

Translating to OpenCL

The natural translation to OpenCL would be to take each step of the summation, and simply compute it, and this would work, as in it would compile and compute, however you would run into the issue of a race condition. That being, for each number being computed, all the other numbers would also being trying to compute. So if we were trying to compute the 10th number in the list, the 7th number also might be trying to compute and we would end up in a non-defined situation, otherwise known as a race condition.

OpenCL is kind to us (atomics) and ensures we don't get inconsistencies on the data structure themselves (imagine if two people tried to write on the same line of paper), however we still have the issue of not knowing the order in which all these numbers are going to be computed on the device. We could introduce a sync point for each number, that is each time we want to compute a number, we have to ensure all the previous numbers are complete. That would work. However it isn't any better than a sequential solution because we would end up waiting a lot and no improvements are made.

Change the Data Dependency

You could get around this race condition by undoing the transformation and simply computing $n_i=\\sum_{k=0}^{i}n_k$ and this would perfectly fine, however it wouldn't become any faster than a sequential version. So the data dependency issue is really what is stopping us from creating a parallel version of the solution that is any better than a sequential one. This doesn't explicitly mean that an OpenCL vs a non-OpenCL version would be any faster, because it does depend on the situation you are in. There is also the consideration of it's possible to do the sequential sum when it is part of a larger parallel algorithm. That is, for any list we're dealing with, just sum the list, even if we've done it before, this does fix the dependency issue however means we're computing the same thing a lot.

We could also just do the naive approach and have each step be the sum of the previous numbers and that might be faster than other solutions for your problem, even though it's Big O complexity is worse O(n^2).

Next Time

In the next post we are going to look at a sub-problem of this, and how to write an OpenCL kernel that partly solves it.