Introduction
In this post I will be going through turning the Painters Partition problem into a parallel solution. The sequential solution to this is a recursive one, and I will show you I how I broke down the problem to turn it into a parallel one.
As always, the code for this is available on GitHub in the "part_2" folder. You can also find a python version of the sequential solution in painters_partition.py.
 crr0004
/
adventures-in-opencl
crr0004
/
adventures-in-opencl
A accompanying repo for my writing about OpenCL
adventures-in-opencl
A accompanying repo for my writing about OpenCL - https://dev.to/crr0004/series/1481
Building
You will need a driver that implements OpenCL 2.0 and cmake.
This was compiled using clang. It should automatically pick up your primary OpenCL vendor and use that.
Headers
The OpenCL headers are included in this repo under shared, if CMake doesn't find them, you can override the directory with "-DOPENCL_INCLUDE_DIRS=../../shared/" when building from one of the build directories. Change the path if it is different for you.
When running it will print out what device is being used but if your vendor implementation is broken it can crash your driver.
Running
Run each sample from the source directory as it needs to pick up the kernel files
Used libraries
- Catch2 https://github.com/catchorg/Catch2
- Google Benchmark https://github.com/google/benchmark/
See LICENSE file for addition of respective licenses
Problem Statement
The problem statement for the painters partition is as follows, "You have to paint N boards of length {A0, A1, A2 … AN-1}. There are K painters available and you are also given how much time a painter takes to paint 1 unit of board. You have to get this job done as soon as possible under the constraints that any painter will only paint continuous sections of board, say board {2, 3, 4} or only board {1} or nothing but not board {2, 4, 5}.", LeetCode (2017).
Basically what it is asking is to find the set of partitions which has the minimum weight. The weight being the maximum sum of each of the partitions. The recursive function can be defined as
that equation is a lot scarier that it looks, and it comes from The Algorithm Design Manual section 8.5 p295, which is also where I originally found the problem.
The part that threw me about the equation was why we are taking the maximum of sum of each part of each set, and it's because the maximum represents how long each painter will take, so we can't do better than the longest painter.
The equation is only one solution to the problem, and you could use other methods but the equation represents the recursive part. The two base cases we need to know are when the sub-set is of length 1 (n=1), and when we have exhausted how many partitions we can have (k=1). When n=1, M[n,k]=n, when k=1, M[n,k]=sum(n), keeping in mind n is the sub-set of numbers we are looking at for the partition.
Moving recursion into OpenCL
Moving something into OpenCL, and hence parallel code, requires establishing what work can be done, and the dependencies between each piece of work.
The two primary ways of thinking about parallel programming is, from a data perspective, or from a task perspective. For the data perspective we take each piece of data and apply the same logic on it, Single Instruction Multiple Data (SIMD). For the task perspective we take a set of data and apply any logic on it, Multiple Instructions Multiple Data (MIMD). Of course these definitions aren't complete and there is more nuance to it, especially when it comes to memory. If you're curious to learn more, you can look at Flynn's Taxonomy.
For our problem we can't directly move the recursive algorithm into a parallel solution because we have a dependency issue.
The primary piece of work we do in the recursive solution is stepping through each partition subset, and the dependency is that each step requires knowing the previous step until we hit a base case, see Line 10 of painters_partition.py.
To get a gist of what I am talking about, I would suggest you run the python file and uncomment line 9 of the python for w to see what is happening. So we have established what work we are doing, and established our dependencies. If can somehow move our dependencies around we can turn this into a parallel version. We won't worry about changing the work we are doing as it turns out we don't need to, it is perfectly valid to though.
The required leap in logic is realising that the recursive step is actually generating unique subsets and then computing on them. What if we could generate these subsets another way?
Recursion to Permutations
I could write another post about figuring out how this recursion can be represented with sets, so instead I will do my best to keep it short in explaining it.
The first step is going back to the problem at hand and establishing that we are doing an exhaustive search for the most optimum arrangement, also read as subsets.
The way the original recursive algorithm does this is by establishing a recursive function to place a separator to create a partition, and then give the remaining partition to same function, further placing another separator, until we hit a base case (run out of separators or one number left). The end result of this is that we can step through all valid permutations for the set.
If you're having trouble convincing yourself of this (like I did), then I would implore you to write a recursive solution yourself and see how it sits together. We can now see how this recursive algorithm is actually generating sets, and so we can treat those as permutations, and then use permutation generation to do the same thing. We don't need to change how we decide the optimum arrangement because it's the same way as the recursive algorithm, take the minimum of the maximum sum. If you understood none of that, which is okay, then just assume that the recursive function is generating sets.
Generating Permutations
If you've spent any time studying algorithms, then you will have come across some form of permutations, and one of my favourite resources for more classical study of algorithms is The Art of Computer Programming, I mainly used this to solve the following problems, mainly Volume 4a.
As we have established that we need unique subsets, we can now transform this problem into something that fixes the dependency issue. We need a sequential algorithm to generate the subsets that doesn't have dependencies.
Buffer or In-Place
In investigating this problem I realised that there were two main ways we could go about generating the permutations to compute on. We can generate the permutation in the OpenCL kernel (therefore no sequential dependencies), or we can pass it in as a buffer. I'm embarrassed to say I spent way too long trying to find a way to generate the permutation from an index, when the answer was on the page I was reading, even though I read the page multiple times.
You can generate the permutation in the OpenCL kernel as you run it. You can do this by using the global index as the permutation index, and using the Theorem L Section 7.2.1.3 The Art of Computer Programming Volume 4a, it is however quite complex to implement. So instead of trying to implement that, I am using Algorithm L of the same section to generate the permutations sequentially and then pass them in as a buffer. This is likely a good spot to check for optimisations. After all, wouldn't it be better if it was all parallel?
Permutation Representation
There are a couple ways to represent the permutation, you could have the set of each painter's section, the length of each painter's section, or the position of the end of each painter's section. I opted for the last one because it means we have permutations without replacement (unique subsets). To get an idea of what I am talking about, take the following example of the set N = {6, 7, 4, 9}, k = 2.
| Sections | Length of Sections | Section End |
|---|---|---|
| {6} {7} {4 9} | 1, 1, 2 | 0, 1 |
| {6} {7 4} {9} | 1, 2, 1 | 0, 2 |
| {6 7} {4} {9} | 2, 1, 1 | 1, 2 |
Implementing in OpenCL
Now we have established what we need, I am going to discuss the actual implementation in OpenCL
Inputs
Buffers
- Permutations of partitions
- Numbers
Constants
- How many dividers
Outputs
- Minimum of the maximum subset sum
- Could also use local memory to improve the performance
Kernel Explained
The title has the link to the Github file, and I am going to be referencing line numbers for the sake of my sanity.
- Line 1-8 - Kernel signature for the function that is going to be invoked
- 2 - buffer in for the permutations of partitions
- 3 - buffer in for the numbers to operate on
- 4 - constant for how many subsets we have (zero indexed)
- 5 - size of the numbers buffer
- 6 - local memory, not really used but could be
- 7 - buffer for the output
- Line 11-12 - The indexes for the kernel in the first dimension (we only ever use the 0th)
- 12 - Local index isn't actually used, I am lazy
- Line 21 - Start index for the subsets we are going to compute on.
- Line 22 - Private max sum for the loops to come
- Line 24 - Private running sum for the loops
- Line 27-30 - The sum for the subset that is from the start of the numbers to the first divider
- Line 31 - Built-in function for maximum number of the inputs
- Line 32 - Reset the running sum
- Line 35-44 - Primary loop for all the partitions that aren't the start or end partitions
- Line 45-51 - The sum for the subset that is from the last divider to the end of the numbers
- Line 57 - Set the output to the minimum of all the maximums of the work items.
- I am very lazy here and use an atomic version the built-in min function so I don't have to deal with any local memory collapsing. This is a very good to optimise as it will block all the other work items.
Executing the Kernel
Actually executing the kernel is fairly straightforward. We just need to generate our permutations, set-up the OpenCL kernel, set-up the buffers and set the kernel to run over an index space. The index space is the permutations vector divided by how many dividers we have set. I mainly use wrapper functions I have written to simply things, however I still use direct OpenCL if they are one line. You can see the documentation for OpenCL function in the reference pages.
One odd thing we have to do is set the output buffer to INT_MAX, so the minimum function works correctly, as the value default to 0.
Performance profiling and optimisation of OpenCL
Unfortunately I won't be going through optimising the C++ and OpenCL code. I might make that a follow up piece though. Optimisation is a rather difficult task, especially when it comes to parallel code. There are however lots of resources out there aimed at general C/C++ optimisation which are still relevant. You can also look at how CUDA code is optimised. I also try to point out spots that you could optimise.
Testing and debugging OpenCL
Lazily I have not written any tests for the program. I should have. Don't do that. Ideally I would even written a test to read in a series of numbers and the excepted output to ensure it's all actually working.
For OpenCL it is harder to test and debug, you are mainly doing black-box testing and debugging. You can do printf out of OpenCL kernels, however the output is flushed at the end of the work item, and so any work item output could come out in any order, which mainly means you need to attached the index to the print statements.
FIN
That's it. You will get a number out which represents our desired output. You can remove the comment on line 83 of main.cpp to hard code the numbers, just remember to set the numbersToGenerate to 4 in main(), and comment out the numbers generation loop (line 86-89 main.cpp)!
I hope this has helped explain how you can think about recursive algorithms in a parallel fashion and use OpenCL to implement it. I know this has taken me awhile to write and I have learnt a lot in doing so. Cheers for reading.

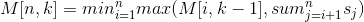

Top comments (0)