Dijkstra's Algorithm
Dijkstra's algorithm (or Dijkstra's Shortest Path First algorithm, SPF algorithm) is an algorithm for finding the briefest ways between hubs in a chart, which may speak to, for instance, street organizations. It was brought about by PC researcher Edsger W. Dijkstra in 1956 and distributed three years after the fact. The algorithm exists in numerous variations. Dijkstra's unique algorithm found the most brief way between two given hubs, however a more normal variation fixes a solitary hub as the "source" hub and finds briefest ways from the source to all different hubs in the diagram, delivering a most brief way tree.
How To use Dijkstra Algorithm:
- Initialize distances according to the algorithm.
- Pick first node and calculate distances to adjacent nodes.
- Pick next node with minimal distance; repeat adjacent node distance calculations.
- Final result of shortest-path tree
What cycle underlies Dijkstra's algorithm?
The cycle that underlies Dijkstra's algorithm is like the ravenous cycle utilized in Prim's algorithm. Tidy's motivation is to locate a base traversing tree that interfaces all hubs in the diagram; Dijkstra is worried about just two hubs.
Dijkstra's Algorithm: Runtime Complexity
•Initialization (clusters, need line) requires some serious energy
•Every reachable hub is embedded and eliminated once from .
•At most Delete Min and addition tasks.
•Each hub is checked all things considered once and each edge is loose all things considered once.
•Implies at most DecreaseKey activity
•Runtime relies upon execution of need line

Fundamentals of Dijkstra's Algorithm
Dijkstra's Algorithm essentially begins at the hub that you pick (the source hub) and it investigates the diagram to locate the briefest way between that hub and the wide range of various hubs in the chart.
The algorithm monitors the at present known most brief good ways from every hub to the source hub and it refreshes these qualities in the event that it finds a shorter way.
When the algorithm has discovered the most brief way between the source hub and another hub, that hub is set apart as "visited" and added to the way.
The cycle proceeds until all the hubs in the chart have been added to the way. Along these lines, we have a way that associates the source hub to all different hubs following the most limited way conceivable to arrive at every hub.
Necessities
Dijkstra's Algorithm can just work with charts that have positive loads. This is on the grounds that, during the cycle, the loads of the edges must be added to locate the most limited way.
On the off chance that there is a negative load in the chart, at that point the algorithm won't work appropriately. When a hub has been set apart as "visited", the current way to that hub is set apart as the most limited way to arrive at that hub. Also, negative loads can modify this if the complete weight can be decremented after this progression has happened.
Bellman–Ford algorithm
The Bellman–Ford algorithm is an algorithm that processes most brief ways from a solitary source vertex to the entirety of the different vertices in a weighted digraph. It is more slow than Dijkstra's algorithm for a similar issue, yet more flexible, as it is fit for taking care of charts in which a portion of the edge loads are negative numbers. The algorithm was first proposed by Alfonso Shimbel (1955), however is rather named after Richard Bellman and Lester Ford Jr., who distributed it in 1958 and 1956, separately. Edward F. Moore additionally distributed a similar algorithm in 1957, and consequently it is likewise in some cases called the Bellman–Ford–Moore algorithm.
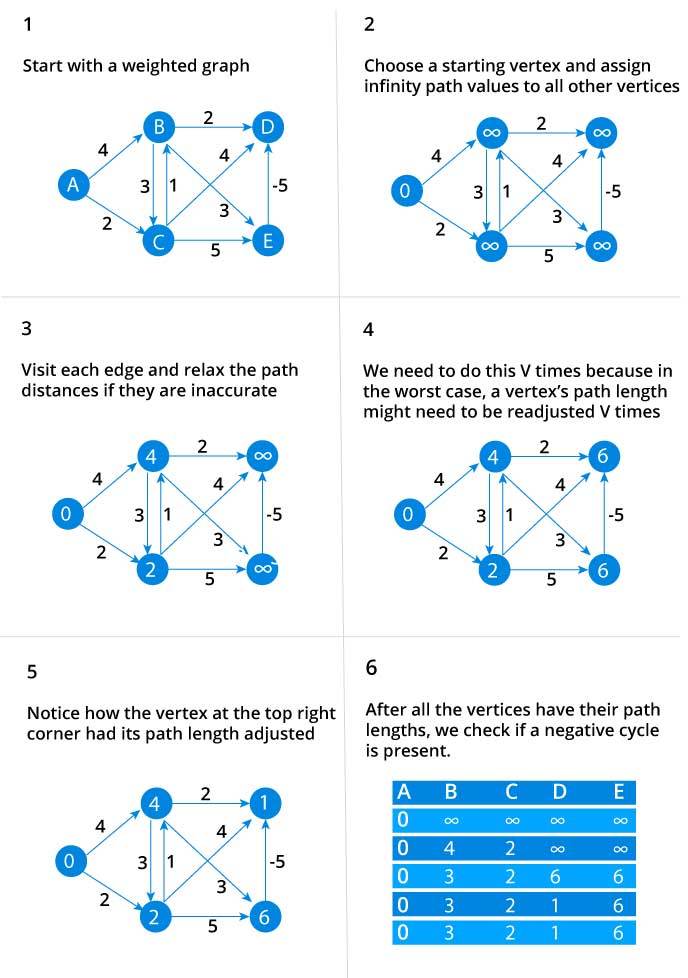
How does Bellman Ford's algorithm work?
Bellman Ford algorithm works by overestimating the length of the way from the beginning vertex to all different vertices. At that point it iteratively loosens up those appraisals by finding new ways that are shorter than the recently overestimated ways.


Top comments (0)