Oi, eu sou o Edu!
Uma das muitas coisas bacanas que aprendi no curso de Big Data de Lousa (lá no Prandiano - Museu da Matemática, em São Paulo/SP) foi a Lei de Newcomb-Benford (ou Lei de Benford, ou ainda, Lei do Primeiro Dígito, como é mais conhecida), e como ela pode ser aplicada para nos ajudar a identificar, por exemplo, possíveis anomalias num processo de auditoria.
Em linhas gerais, a Lei trata de um fenômeno que diz que há uma probabilidade de, num conjunto de números quaisquer não-aleatórios, o número 1 ocorrer um maior número de vezes que o número 2, e este ocorrer mais vezes que o 3, e assim sucessivamente, até o 9.
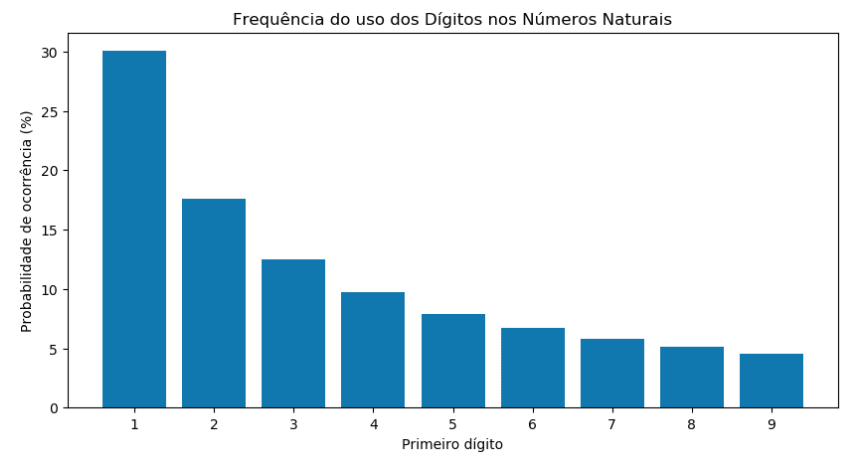
Neste post não entrarei em detalhes sobre tal fenômeno (e nem sobre as observações do astrônomo Newcomb e do físico Benford relativas a ele), mas deixarei os links para seus respectivos artigos ao final do texto. O fato é que o fenômeno é real, e a probabilidade de cada um dos números de 1 a 9 aparecer como primeiro dígito pode ser demonstrada através do gráfico a seguir, e verificada a partir de um cálculo logarítmico.
Como pode ser observado no gráfico, a probabilidade da ocorrência do número 1 no primeiro dígito é de cerca de 30%, enquanto que a da ocorrência do número 9 é de aproximadamente 4%. Mas... como se calcula isso? E, mais importante, o que podemos fazer com estes dados?
Para calcular a probabilidade de frequência da ocorrência de cada número como primeiro dígito, é possível utilizar a seguinte expressão matemática (onde d corresponde a cada um dos dígitos de 1 a 9):
Aplicando a expressão ao número 1, obtém-se sua sua probabilidade de ocorrência como primeiro dígito em percentual, ou seja, 30,10%. Para o número 2, a probabilidade dele aparecer como primeiro dígito cai para 17,60%. E, para o número 3, pode-se verificar que há somente 12,49% de chance dele aparecer no primeiro dígito!
É muito legal isso, né?
Mas... e como usar toda essa informação para nos ajudar a identificar possíveis anomalias num processo de auditoria, como escrevi lá em cima? Bem, irei escrever sobre isso no próximo post. ;)
Espero que tenham gostado do texto (comentários, críticas e sugestões são sempre bem-vindos), e que voltem aqui outras vezes.
Grande abraço, e até a próxima!
Ah, já ia me esquecendo:
O astrônomo Simon Newcomb foi quem primeiro observou o fenômeno que descrevi no post, e publicou suas observações num artigo chamado "Note on the Frequency of Use of the Different Digits in Natural Numbers" no American Journal of Mathematics (Vol. 4, No. 1, pp. 39-40 ), em 1881.
Em 1938, o físico Frank Benford também percebeu tal fenômeno, publicando suas observações no American Philosophical Society (Vol. 78, No. 4, pp. 551-572), no artigo intitulado "The Law of Anomalous Numbers".

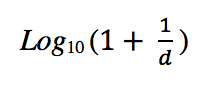

Top comments (0)