Sorting is the process of arranging a collection of elements in a specific order. In programming, sorting is a fundamental concept as it allows us to organize data in a way that makes it easier to search, analyze, and process.
Sorting helps in improving the efficiency of various algorithms and operations. It is particularly important when dealing with large datasets, as it enables faster retrieval and manipulation of information.
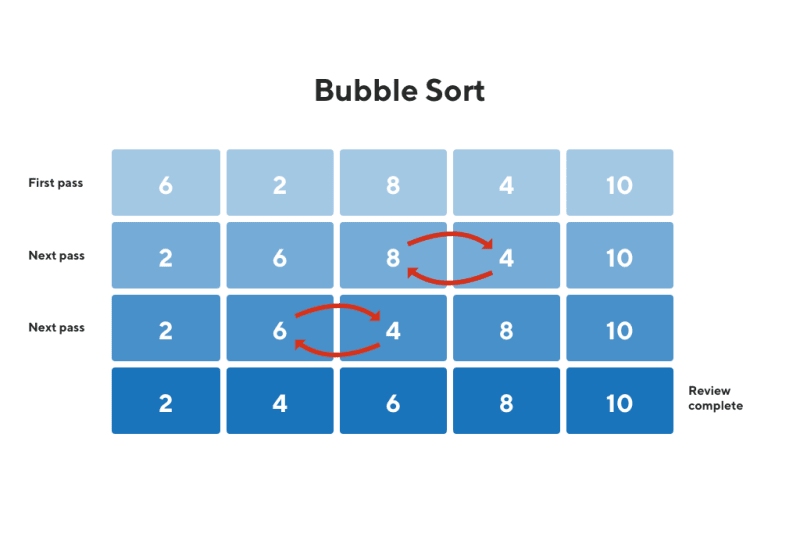
The bubble sort algorithm is a simple and commonly used sorting technique in computer science. It works by repeatedly swapping adjacent elements in a list until the entire list is sorted. This algorithm gets its name from the way smaller elements "bubble" to the top of the list.
Bubble sort is easy to understand and implement, making it a popular choice for introductory programming courses. However, it is not the most efficient sorting algorithm, especially for large data sets. Despite its limitations, bubble sort is still useful in certain scenarios and serves as a good starting point for understanding sorting algorithms.
In this article, we will explore the implementation of the bubble sort algorithm for sorting a 2D array in Java. The bubble sort algorithm is a simple sorting algorithm that repeatedly compares adjacent elements and swaps them if they are in the wrong order. This article will provide a step-by-step guide on how to implement the bubble sort algorithm in Java for sorting a 2D array.
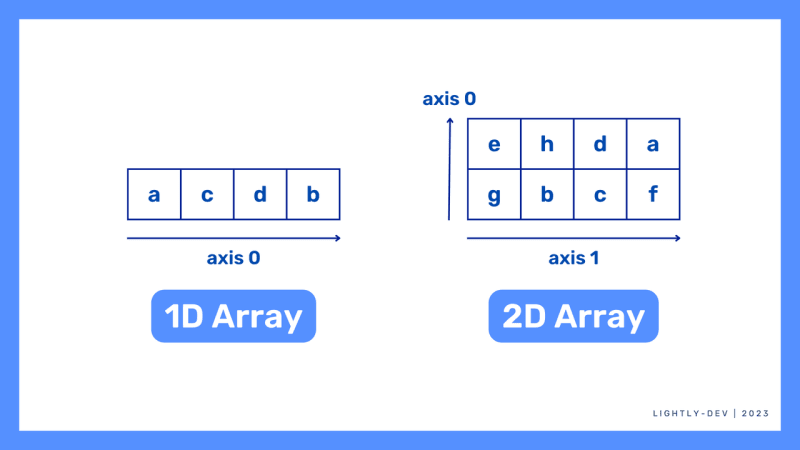
What is a 2D Array in Java?
A 2D array, also known as a two-dimensional array, is a data structure that allows for the storage of values in a grid-like format with rows and columns. Unlike a regular 1D array, which is a linear collection of elements, a 2D array represents data in a tabular form.
In a 2D array, each element is accessed using two indices - one for the row and another for the column. This provides a way to organize and manipulate data that has a two-dimensional nature, such as a matrix or a grid. In contrast, a regular 1D array only requires one index to access its elements.
In a 2D array, also known as a matrix, the data is organized in rows and columns. The rows represent the horizontal aspect of the array, while the columns represent the vertical aspect.
Each element in the array is accessed using its row and column index. The number of rows and columns in a 2D array determine its dimensions. Rows are usually numbered from top to bottom, starting from 0, and columns are numbered from left to right, also starting from 0. The concept of rows and columns in a 2D array allows for efficient storage and retrieval of data in a structured manner.
A 2D array is a useful data structure that can be used to represent various types of data. Here are some examples:
- Pixel values in an image: A 2D array can be used to represent an image, where each element of the array stores the pixel value at a specific location. The rows and columns of the array correspond to the height and width of the image, respectively.
- Student grades: A 2D array can be used to store the grades of multiple students in different subjects. Each row in the array represents a student, and each column represents a subject. The elements of the array can store the corresponding grades for each student-subject combination.
- Game board: A 2D array can be used to represent a game board, such as a chessboard or a tic-tac-toe grid. Each element of the array can represent a position on the board, and its value can indicate the state of that position (e.g., empty, occupied by a player).
- Temperature readings: A 2D array can be used to store temperature readings at different locations over a period of time. Each row in the array represents a specific location, and each column represents a specific time interval. The elements of the array can store the corresponding temperature values.
These examples demonstrate how a 2D array can be used to organize and represent data in a structured manner, allowing for efficient manipulation and analysis.
Bubble Sort Algorithm in Java
The bubble sort algorithm is a simple sorting algorithm that works by repeatedly swapping adjacent elements if they are in the wrong order. It gets its name because smaller elements "bubble" to the top of the array with each iteration. The basic steps of the bubble sort algorithm are as follows:
- Start with an unsorted 2D array.
- Compare the first two elements. If the first element is greater than the second element, swap them.
- Move to the next pair of elements and repeat step 2.
- Continue this process until the entire array is sorted.
- Repeat the above steps for each row of the 2D array.
- Finally, the 2D array will be sorted in ascending order.
The Bubble Sort algorithm compares adjacent elements in a 2D array and swaps them if they are in the wrong order. It starts by comparing the first element with the second element. If the first element is greater than the second element, they are swapped. Then, it moves on to compare the second element with the third element, and so on, until it reaches the end of the array.
This process is repeated for each row of the 2D array. The algorithm continues this comparison and swapping process until the entire array is sorted in ascending order. By comparing adjacent elements and swapping them if necessary, the Bubble Sort algorithm gradually moves the larger elements towards the end of the array, resulting in a sorted 2D array.
The time complexity of bubble sort is O(n^2), where n is the number of elements in the array. This means that bubble sort is not very efficient for large arrays.
However, bubble sort can be suitable for small arrays or partially sorted arrays. In a small array, the overhead of more complex algorithms may outweigh the benefit of their faster time complexity. Additionally, bubble sort performs well on partially sorted arrays because it only requires a few passes to complete the sorting process. Therefore, bubble sort can be a reasonable choice when dealing with small arrays or arrays that are already partially sorted.
Sorting a 2D Array using Bubble Sort in Java
To implement the bubble sort algorithm, we iterate through each row of the 2D array. Within each row, we compare adjacent elements and swap them if they are in the wrong order. This process is repeated until no more swaps are needed, indicating that the array is fully sorted.
The bubble sort algorithm has a time complexity of O(n^2), where n is the total number of elements in the array. This makes it suitable for small arrays or when simplicity of implementation is more important than efficiency.
Once the sorting process is complete, the 2D array will be arranged in ascending or descending order, depending on the sorting criterion used.
To perform bubble sort on a 2D array in Java, the following steps can be followed:
- Iterate through each row of the array using nested loops. The outer loop will iterate through the rows, and the inner loop will iterate through the columns of each row.
- Compare adjacent elements within each row and swap them if they are in the wrong order. This can be done using another nested loop. Start from the first element of each row and compare it with the next element. If the next element is smaller, swap them. Continue this process until the last element of the row.
- Repeat the above step for each row of the array. This will ensure that all elements within each row are in the correct order.
- After completing the above steps for each row, repeat the entire process for a number of iterations equal to the number of rows in the array. This will ensure that all rows are sorted within the 2D array.
This is a code snippet demonstrating the implementation of bubble sort for a 2D array in Java:
public class BubbleSort2DArray {
public static void bubbleSort(int[][] arr) {
int rows = arr.length;
int columns = arr[0].length;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns - 1; j++) {
for (int k = 0; k < columns - j - 1; k++) {
if (arr[i][k] > arr[i][k + 1]) {
int temp = arr[i][k];
arr[i][k] = arr[i][k + 1];
arr[i][k + 1] = temp;
}
}
}
}
}
public static void main(String[] args) {
int[][] array = {
{4, 2, 6},
{1, 5, 3},
{9, 7, 8}
};
System.out.println("Before sorting:");
for (int[] row : array) {
for (int element : row) {
System.out.print(element + " ");
}
System.out.println();
}
bubbleSort(array);
System.out.println("After sorting:");
for (int[] row : array) {
for (int element : row) {
System.out.print(element + " ");
}
System.out.println();
}
}
}
This code snippet demonstrates the implementation of the bubble sort algorithm for sorting a 2D array in Java. The bubbleSort method takes a 2D array as input and sorts each row of the array in ascending order using the bubble sort algorithm. The main method initializes a 2D array and calls the bubbleSort method to sort the array. It then prints the array before and after sorting.
Sorting a 2D Array of Integers in Java
In a hypothetical scenario, let's consider a digital image processing application that requires sorting a 2D array of pixel intensities. Each pixel is represented by an integer value, indicating its brightness or color intensity.
The 2D array represents an image, where the rows and columns correspond to the pixel coordinates. Sorting this 2D array would be useful in various scenarios, such as enhancing image contrast, identifying patterns or objects based on pixel intensities, or performing mathematical operations on the image data.
In order to efficiently process and analyze the image data, sorting the 2D array would provide a well-organized and consistent representation of the image's pixel intensities.
Below is an example of an initial unsorted 2D array in Java:
int[][] array = {
{4, 2, 7},
{1, 5, 3},
{9, 6, 8}
};
In this example, the 2D array consists of 3 rows and 3 columns. The values within the array are not in any particular order and need to be sorted using the Bubble Sort algorithm.
To sort a 2D array using the bubble sort algorithm in Java, we follow a step-by-step process:
- Firstly, we initialize a boolean variable swapped to keep track of whether any elements were swapped during each iteration.
- We start with the outer loop, which will run for n-1 iterations, where n is the number of rows in the 2D array.
- Inside the outer loop, we have an inner loop that compares adjacent elements in each row and swaps them if they are in the wrong order. We iterate until n-1-i elements in each row have been compared, where i is the current iteration of the outer loop.
- During each iteration of the inner loop, if a swap is made, we set the swapped variable to true.
- After completing each iteration of the inner loop, we check the value of swapped. If it is still false, it means no swaps were made in that iteration, indicating that the array is already sorted. In this case, we break out of the outer loop.
- Finally, we print the sorted 2D array.
The bubble sort algorithm works by repeatedly swapping adjacent elements if they are in the wrong order. In each iteration, the largest element in the unsorted portion of the array "bubbles" up to its correct position. This process continues until the array is fully sorted.
To display the final sorted 2D array using the Bubble Sort algorithm in Java, we can iterate over each element of the array and print them in a formatted manner. Here is an example code snippet to achieve this:
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
In the above code, arr represents the 2D array that has been sorted using the Bubble Sort algorithm. The outer loop iterates over each row, while the inner loop iterates over each column of the array. Each element is printed followed by a space, and at the end of each row, a new line is printed to display the next row of the array.
Best Practices and Optimization When Using Bubble Sort
When implementing the bubble sort algorithm, there are a few best practices that can help improve its efficiency. Firstly, it is important to set a flag to check if any swaps occur during a pass. If no swaps are made, it means that the array is already sorted, and the algorithm can terminate early. This optimization can significantly reduce the number of iterations required.
Additionally, it is recommended to use a modified version of bubble sort called the "optimized bubble sort" which starts from both ends of the array. This approach can further reduce the number of comparisons and swaps needed. Lastly, it is crucial to consider the time complexity of bubble sort, which is O(n^2). For large arrays, it is advisable to use more efficient sorting algorithms such as quicksort or mergesort.
Learn Java Programming with Java Online Compiler
Are you struggling with solving errors and debugging while coding? Don't worry, it's far easier than climbing Mount Everest to code. With Lightly IDE, you'll feel like a coding pro in no time. With Lightly IDE, you don't need to be a coding wizard to program smoothly.
One of its notable attributes is its artificial intelligence (AI) integration, enabling effortless usage for individuals with limited technological proficiency. By simply clicking a few times, one can transform into a programming expert using Lightly IDE. It's akin to sorcery, albeit with less wands and more lines of code.
For those interested in programming or seeking for expertise, Lightly IDE offers an ideal starting point with its Java online compiler. It resembles a playground for budding programming prodigies! This platform has the ability to transform a novice into a coding expert in a short period of time.
Read more: A Comprenhensive Guide on Bubble Sort For 2D Array in Java




Top comments (0)