As is the case with a lot of topics in programming, there is always more than one way to do something, and this can often make things really confusing. Having failed a technical interview, I realized how important to be able to recognize and properly categorize the type of problem and the solution that is most effective for the situation. Time is of the essence in these industries, as a microcosm of what is to be expected as a developer. In an effort to expand my arsenal, I've decided that I really need a grasp of popular grasps, so that I can expand my arsenal and know which ones excel in particular situations. For this I decided that I finally want to understand the differences between recursion and iteration.
The first thing I was surprised to find is that anything that is recursive can be solved using an iterative function, and vice versa. Being comfortable with iteration, after learning this I was tempted to simply continue using the familiar iterative approaches that I have been using already. However, there are some distinct advantages to both approaches. I'm assuming that most people are like me and that they are less familiar with the recursive approach, given how abstract it is. My goal for this article will be to show why and how the recursive method can be prefereable.
What is Recursion?
First the most basic definition of a function that uses recursion is simply that it calls itself. Essentially, just as loop does an operation multiple times, recursion also functions in a similar fashion. It helps to think of the recursive function as the same thing as whatever happens during each iteration.
However, there's a problem that arises when this function can't stop calling itself. Just like you don't want the iterative function to continue to loop until i < infinity, you would always need to have a base case. In the case of our iteration, we usually set some condition like i < 3 in order to indicate how many times we want i to increment and do the operations in the function. Similarly, we would set a condition in a recursion function as well and this will actually result in returning a value, thus resolving that current function call.
Before we dive into the specifics, here's a list of advantages and disadvantages.
Advantages
- Recursion offers elegant solutions that are easier to understand
- Can solve more complex problems than with just iteration.
Disadvantages
- Requires more space, because you need to add to the stack for every recursive call
Recursion power lies in the utilization of the call stack
So the main question, that I've been trying to answer is why is recursion used, and one of the advantages that we listed was that recursion can solve more complex problems. Why is this so? To demonstrate this, I want to use two different approaches to solving a familiar algorithm in DFS, to attempt to explain the different utilities between the two functions.
function traverseDFS(root) {
let stack = [root]
let res = []
while (stack.length) {
let curr = stack.pop()
res.push(curr.key)
if (curr.right){
stack.push(curr.right)
}
if (curr.left){
stack.push(curr.left)
}
}
return res.reverse()
}
This is the iterative version of a DFS search algorithm. In this algorithm, we are pushing to a stack, which is an essential portion of doing a 'complex' problem like a binary search tree traversal. Everytime have something in the stack, which is a node, we need to check whether that iteration is going to have a right and a left node. After encountering a situation where there is a left and right node, we need to be able to recall the possibility that there might be another right and left node in the previous right and left nodes we encountered.
A stack can help us do this, by keeping track of every potential right and left node on that stack, and then running through the entire stack and running the same checks on all those potential nodes. Also, since this a DFS traversal, we'll need to use the pop method, to check the most recent item that was put onto the stack(the deepest element first search). This actually also forces us to use a reverse function if we wanted it to check the left side first, since it reverses that as well.
let recursiveBFS = (root) =>{
if(root.right){
console.log('right', root.right.value)
recursiveBFS(root.right)
}
console.log(root.value)
if(root.left){
console.log('left', root.left.value)
recursiveBFS(root.left)
}
}
On the contrary, here is the much simpler method of using recursion in order to do a DFS traversal. In this case, everytime we either run into a right or left node, we're adding another function onto a call stack. So you can imagine that when we first start with a root node, we encounter a right node, then we add that recursiveBFS function onto the stack and we execute it immediately. Until we reach right nodes this will keep happening.
Remember though, even if the binary search tree continues to have right nodes, the first right node is still on the call stack. This is, because it has not yet console logged its value, and it has not checked for whether there is a left node yet. So, it waits for the last right node to be reached at which point, that will encounter no other right nodes, execute the console log, check for a left node, and finish executing when there is nothing left.
What is so great about recursion is you did not need to keep track of that, but as I said earlier the power of recursion lies in the call stack. Whereas, we needed to create one from scratch earlier, we can no store that on the call stack itself. This allows for more complicated function calls as it saves your function on the call stack, until the rest of your iterations finish an intial function, and then finally completing execution when a desired endpoint is reached for all requirements.
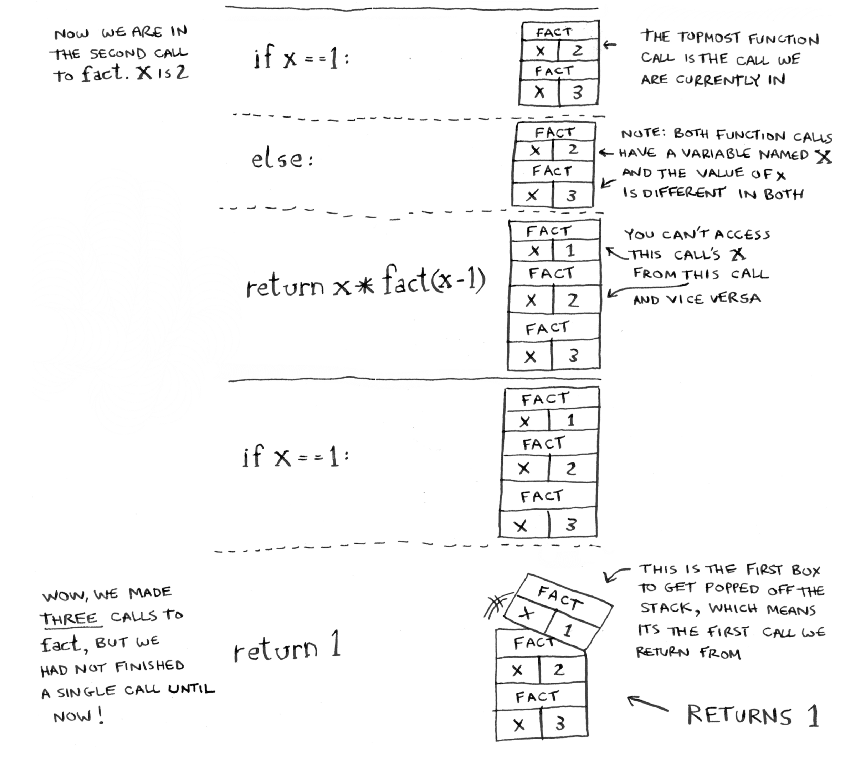
I'm not sure if I explained very clearly, but I think this diagram has been very helpful. This diagram essentially displays whats happening on the stack, when you are performing recursion. The problem that's being displayed here is the famous fibonacci recursion problem.
You'll notice that everytime we run into another call of the function, we put that function call onto the top of the stack. Depending on the function that is being called, that function call will remain on the stack until it is finished running. In this case, each function has another call of the function but with the previous input minus 1. Once we reach the base case, we can see how the stack finishes the function call and pops it off the stack.
Recursion is pretty confusing, and there's still many other examples which I haven't looked into yet, but I thought this would show a small bit of potential. There's also great potential for recursion in graphs, which can make recursive calls to a function without the right and left check, but instead for every neighbor, and then every neighbor of that neighbor.


Top comments (0)