Depth-First Search

🔁Quick BFS Recap

• In Breadth-First Search (BFS), you explore the graph level by level.
• You visit all immediate neighbors first, then move on to their neighbors, and so on.
• Uses a queue (FIFO)
• Best for shortest path in unweighted graphs
• Real-life: friend suggestions, web crawling, peer-to-peer networks

Now, Let’s Dive into DFS – Depth-First Search

• No more level-by-level. It’s time to go DEEP!
• In DFS, you pick a path and go as deep as possible, only backtracking when there’s nowhere left to go.

Let's Imagine this,

You enter a maze and just keep walking forward till you hit a dead-end, then backtrack and explore the next path.

It Uses recursion or a stack and best for the Exploring complete paths, Detecting cycles, Maze solving, Topological sort.

What is DFS?
Depth-First Search (DFS) is a classic graph traversal algorithm.
Instead of exploring layer by layer like BFS, it dives deep into each branch of a graph or tree before backtracking.

How It Works:

1.Start from a source node

• Choose a node to begin with (say, node 0).
• This will be the root of your traversal.

2.Use a stack (or recursion) to track the path

• DFS relies on a stack data structure.
• You can either explicitly use a stack or let recursion handle it for you (since function calls internally use a call stack).

3.Maintain a visited[] array

• To avoid infinite loops (especially in cyclic graphs), keep track of nodes you’ve already visited.
• This ensures each node is processed only once.

4.Process nodes deeply before backtracking

• Visit the current node and mark it as visited.
• Then, move to its first unvisited neighbor.
• Continue this process until there are no unvisited neighbors left.
• When stuck, backtrack to the most recent node that still has unvisited neighbors, and repeat.

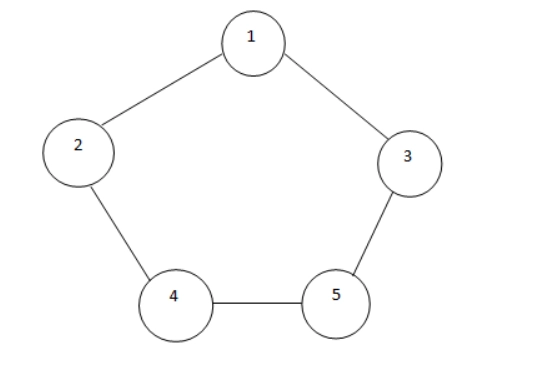
🧠 Graph Structure (Adjacency List based on the image):
From the graph:
1: [2, 3]
2: [1, 4]
3: [1, 5]
4: [2, 5]
5: [3, 4]

We’ll assume:
It’s an undirected graph.

Step 1

• Start DFS at 1.
• Mark 1 as visited → Visited = [1].
• Explore first neighbor → 2.

Step 2

• At node 2.
• Mark 2 as visited → Visited = [1, 2].
• Explore first neighbor → 4.

Step 3

• At node 4.
• Mark 4 as visited → Visited = [1, 2, 4].
• Neighbors of 4 = (2, 5).
  • 2 already visited → skip.
  • Move to neighbor 5.

Step 4

• At node 5.
• Mark 5 as visited → Visited = [1, 2, 4, 5].
• Neighbors of 5 = (3, 4).
  • 4 already visited → skip.
  • Next is 3.

Step 5

• At node 3.
• Mark 3 as visited → Visited = [1, 2, 4, 5, 3].
• Neighbors of 3 = (1, 5). Both already visited → backtrack.

Step-by-Step (Recursive DFS)
Start at 1, mark visited → dfs = [1]
Go to neighbor 2 (first unvisited of 1) → dfs = [1, 2]
Go to neighbor 4 (from 2) → dfs = [1, 2, 4]
Go to neighbor 5 (from 4) → dfs = [1, 2, 4, 5]
Go to neighbor 3 (from 5) → dfs = [1, 2, 4, 5, 3]
All neighbors visited. Backtrack until all paths are done.

🔄 Final DFS Traversal Order:
1 → 2 → 4 → 5 → 3

DFS Code in C++

#include <iostream>
#include <vector>
using namespace std;

// Helper method to perform DFS recursively
void dfsHelper(int node, vector<int> adj[], vector<bool>& visited, vector<int>& dfs) {
    visited[node] = true;
    dfs.push_back(node);

    for (int neighbor : adj[node]) {
        if (!visited[neighbor]) {
            dfsHelper(neighbor, adj, visited, dfs);
        }
    }
}

// DFS function that calls the helper
vector<int> dfsOfGraph(int V, vector<int> adj[]) {
    vector<int> dfs;
    vector<bool> visited(V, false);
    dfsHelper(0, adj, visited, dfs); // starting from node 0
    return dfs;
}

int main() {
    int V = 5;
    vector<int> adj[V];


    // 1-2, 1-3, 2-4, 3-5, 4-5
    adj[0] = {1, 2};    // node 1 -> 2, 3
    adj[1] = {0, 3};    // node 2 -> 1, 4
    adj[2] = {0, 4};    // node 3 -> 1, 5
    adj[3] = {1, 4};    // node 4 -> 2, 5
    adj[4] = {2, 3};    // node 5 -> 3, 4

    vector<int> result = dfsOfGraph(V, adj);

    cout << "DFS Traversal: ";
    for (int node : result)
        cout << node + 1 << " ";  
    cout << endl;

    return 0;
}

⏱ Time Complexity → O(V + E)

• V (Vertices):

  • Every vertex is visited exactly once.
  • Visiting a node + marking as visited = O(1) each → overall O(V).

• E (Edges):

  • For every node, DFS explores its adjacency list (all connected edges).
  • Across the whole graph, each edge is checked at most twice (once from each endpoint in an undirected graph, once in a directed graph).
  • Total edge exploration = O(E).

So, the total time = O(V + E).

Space Complexity → O(V)
DFS requires memory for:

• Visited array → To keep track of visited nodes (size = V).
• Recursion stack (or explicit stack) →
• In the worst case (graph shaped like a linked list), recursion depth can go up to V.

So, maximum call stack size = O(V).