🔍 Let's Find It – Binary Search! 🚀

🧠 The Magic of Smart Searching
A Tale of Sorted Boxes & Smart Moves
A Tale of Two Halves: The Smart Snack Box 🍫
You're back in your room and spot your snack stash – but this time
it’s super organized.
All your chocolates are sorted in alphabetical order:
[5-Star, Dairy Milk, KitKat, Munch, Perk]
Now, you want to grab your fav – Munch.
But wait! 🤔 Instead of checking each one (like in linear search),
you’ve got a smarter plan this time!

🧠 What is Binary Search?
Binary Search is like being a smart detective in a sorted list.
Rather than checking one-by-one, you go straight to the middle!
You divide and conquer!
Cut the list in half
🔍 Check the middle item
👉 Decide: Go left? Or go right?
Repeat till you find it (or not)!

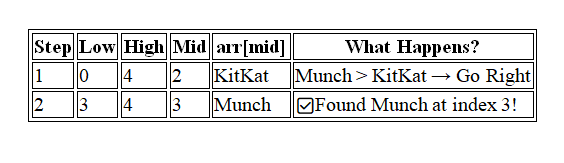
🎯 Let’s Do a Dry Run:
Snack box = [5-Star, Dairy Milk, KitKat, Munch, Perk]
You're searching for Munch 🍫
Let’s turn the story into steps:

❓ What if it’s not there?
Snack box: [5-Star, Dairy Milk, KitKat, Munch, Perk]
You search for Snickers 🍫 (not in list)
You do the same process:
Middle = KitKat → not Snickers
Move right or left → check → still not there ❌
Eventually, you return -1 = Not Found.

📌 Steps to Remember:
Check if the array is sorted ✅
Set two pointers → low and high
While low <= high:
Find mid = (low + high)/2
Is it the target? → 🎯 Return index!
If target < mid → Move high = mid - 1
If target > mid → Move low = mid + 1
If not found → return -1 ❌

🧑‍💻 Code Time! (C++)

int binarySearch(vector<string>& arr, string target) {
    int low = 0, high = arr.size() - 1;

    while (low <= high) {
        int mid = low + (high - low) / 2;

        if (arr[mid] == target)
            return mid;
        else if (arr[mid] < target)
            low = mid + 1;
        else
            high = mid - 1;
    }

    return -1; // Not Found
}

💡 Quick Recap:
✅ Binary Search works only on sorted arrays
Cut the search space in half every time
⚡ Time Complexity: O(log n)
🚀 Way faster than Linear Search!
Real-World Analogy:
Imagine finding a name in a phone book 📖
Do you start from page 1?
Nope! You flip to the middle 📖 → Then go left or right!
That’s Binary Search 💡

💬 Wrapping Up
Binary Search is like Sherlock Holmes — it doesn’t check everything, it thinks, splits, and finds smartly!
So next time you’re searching something in a sorted list —
Don't be slow… go Binary! 🧠