Ok, back to earth. Spending too long building an elaborate and unnecessary solution like last time takes too long, so I'll keep this one simple.
The Challenge Part 1
Link to challenge on Advent of Code 2020 website
The challenge is another one where we must break a code. Quite simply, in a list of numbers, a number can be made from adding together two of the previous n numbers before it. Find the one that doesn't follow this rule.
Re-using Day 01
This problem is actually pretty similar to the Day 01 challenge, which involves finding two numbers out of a list that adds up to the first. To save time, we can just re-use that:
from itertools import combinations
for left_number, right_number in combinations(data, 2):
if left_number + right_number == 2020:
print("Found it!", left_number, right_number)
break
This code finds a pair of numbers out of an list that add up to 2020. We just need to adjust this a bit. Firstly, we need to replace data with a "slice" of the original list. If we call the value we're checking idx, then we need to slice from 25 before that up to 1 before it. This can be done using the python slice notation data[idx-preamble:idx]. Secondly, we need to compare the numbers with the value data[idx], so:
for left_number, right_number in combinations(data[idx-preamble:idx], 2):
if left_number + right_number == data[idx]:
break
Next, this just needs to go in a loop, and we need to detect when it doesn't break, which thankfully is easy in Python as for loops also have an else clause that triggers if you complete the loop without breaking. Since we're looking for a number where no combination exists, it won't break out of the loop, and therefore we can catch it.
This is the full code for Part 1
data = [int(line) for line in open("input.txt").readlines()]
preamble = 25
for idx in range(preamble, len(data)):
for left_number, right_number in combinations(data[idx-preamble:idx], 2):
if left_number + right_number == data[idx]:
break
else:
print("Did not find it!", start, data[idx])
The Challenge Part 2
Part 2 of the challenge, asks us to find the sum of any continuous range of numbers that add up to the number found in Part 1, which I shall name the_number. Essentially the problem boils down to this: we have 1000 numbers in data, let's define X as the starting position, and Y as the ending position between which to sum the values. Find X and Y that result in a sum equal to the_number.
Unlike previous challenges in which brute-force was an option, this is now brute-forcing along two different axes. Since we have 1000 numbers, we have slightly under 1000*1000/2 = 500,000 iterations to go through (it's less than half because the one constraint is X should be lower or equal to Y)
Vectorizing the solution
We can consider the search space a big 2D array, with values 0 to 1000 on each axis, giving us a bit over a million entries. About half of these values are invalid due to the constraint that X<Y.
The easiest way to vectorize the brute-forcing of this solution is again to use numpy. Let's first load the data using numpy:
import numpy as np
data = np.loadtxt("input.txt")
Next, I'm going to define a function that takes the start point, the end point, and returns a value that represents how close we are to the target. It's basically the difference between the result and the number we want, such that when the value is 0, we know we have the right value.
def sum_range_err(start, end):
if 0 <= start < end < data.size):
return np.abs(the_number - np.sum(data[int(start):int(end)]))
return np.NaN
Here, I define the constraint that the start must be lower than the end, and both must be between 0 and the size of the data, and anywhere outside the constraint is np.NaN.
Unfortunately because of the way this function works, it cannot take vectors as inputs like I can with arithmetic, for example, A+B when both A and B are vectors works great, the result is another vector where each element has been added together. However, data[A:B] will not result in a vectorized calculation simply because numpy doesn't know how to do this. Without thinking too much about it, I'm just going to throw the whole function into numpy's numpy.vectorize() function which wraps my function for me so I don't have to think about it. The return value is now a vectorized version of my function that will run itself on each member of input vectors.
sre = np.vectorize(sum_range_err)
While sum_range_err() can only take single integers for its arguments, this new function sre() can take two vectors and return a vector. This helps speed things up.
Now, onto calculating our grid of values. To do so, I just need to calculate an array of the inputs, simply all the values between 0 and the size of our data, and then pass them through our sre function to get a grid of results. That's all!
xax = yax = np.arange(0, data.size)
zvals = sre(xax[:,None], yax[None,:])
Finally, we just need to find where zvals is zero:
print(np.where(zvals == 0))
The full code:
import numpy as np
data = np.loadtxt("input.txt")
def sum_range_err(start, end):
if 0 <= start < end < data.size:
return np.abs(the_number - np.sum(data[int(start):int(end)]))
return np.NaN
sre = np.vectorize(sum_range_err)
xax = yax = np.arange(0, data.size)
zvals = sre(xax[:,None], yax[None,:])
print(np.where(zvals == 0))
Output
(array([554, 667]), array([571, 668]))
This code only takes a few seconds to run (4 seconds on my machine) thanks to numpy's optimization, and we didn't have to think too much about how to write or optimize the code.
We could make this faster, by optimizing the access to the data, as well all the options I discussed in Day 01 (cupy, numba, etc.)
The result is two ranges: 554:571 and 667:668. The second range is actually just the Part 1 solution - we were looking for any range that sums to the entry we found in Part 1. So naturally, a range consisting of just the entry itself has a sum equal to itself.
Plotting stuff
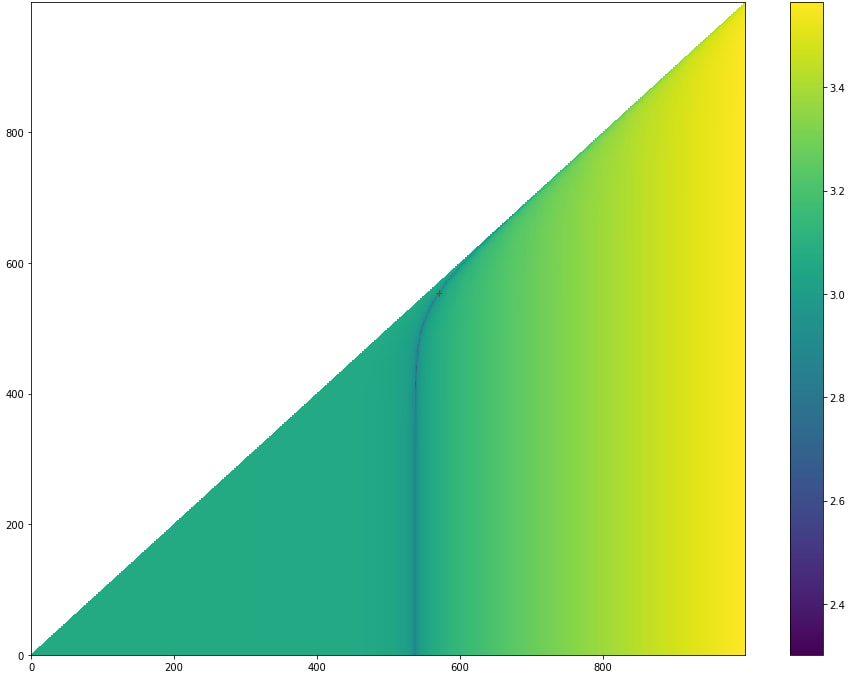
The zvals calculated above is a 2D grid of data values, and we're looking for the minima of this value. We can easily visualize what this looks like using matplotlib by plotting a colour map:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16,12))
cplot = ax.pcolormesh(xax, yax, np.log(np.log(zvals)))
fig.colorbar(cplot)
ax.plot(resultx, resulty, 'r+')
fig.show()
Here, I've applied a couple of log functions to the z values to make the colours look clearer. The graph is actually very steep, which makes it difficult to see clearly, and also presents a challenge for any gradient-based optimization method.
I've also plotted the result point as a red plus sign to highlight where it is.
What we can see here is that the correct value is in a very narrow valley of numbers. This valley is so narrow, that I actually tried some optimization/minimization functions from the scipy package, and most of them failed to find the solution. The only success was the brute-force method, which took many times longer than the vectorized version above. I think those optimization functions would probably still work but would take some fine-tuning to get the step sizes correct.
Here's that brute-force code:
from scipy import optimize
def sum_range_err_reflected(point):
start = np.min(point)
end = np.max(point)
return np.log(np.log(np.abs(the_number - np.sum(data[int(start):int(end)]))))
ranges = (slice(0, data.size, 1), slice(0, data.size, 1))
optimize.brute(sum_range_err_reflected, ranges=ranges)
Note, I rewrite the function to reflect the results along x=y (see the plot in the cover image), to give it a full graph to work with, since optimize.brute() does not handle NaN values.
This takes about 20 seconds on my machine, versus the 4 seconds of the plain old vectorized method. Using a better global optimization strategy should work faster, and if well-tuned, is likely to easily beat 4 seconds. Also, it's worth mentioning that 4 seconds is itself really slow, and an optimized version of even a brute-force should solve faster than that. The reason for this is though numpy's vectorized calculations are fast, we're pulling that back into Python, and going through a python function, so we're incurring a large amount of python function execution overhead. Re-writing that vectorized array access in numpy would allow us to do much better.
Onwards!



Top comments (0)