Another opportunity to pull out that PEG grammar for parsing, this time I'm pleased to have an opportunity to dig into a new library I've not used before, NetworkX, a powerful graph library (the datastructure kind, not the drawing kind) for Python.
Things mentioned in this post: Parsing Expression Grammars (PEG), graph theory, directed acyclic graphs (DAGs), NetworkX library, graph traversal, recursive functions
The Challenge Part 1
Link to challenge on Advent of Code 2020 website
The challenge presented is in reality a tree/graph traversal problem. You are presented with a large set of "rules" that define what "colour" bag can contain what other "colour" bags.
For example, take two of the example rules:
light red bags contain 1 bright white bag, 2 muted yellow bags.
bright white bags contain 1 shiny gold bag.
Fundamentally, this means that "light red" is the parent of "bright white", and the parent of "muted yellow". And in the second line, "bright white" is the parent of "shiny gold". Combining these two rules together, we can say that "light red" is a grandparent of "shiny gold"
Diagrammatically, as a tree:
Light Red
|
|--Bright White
| |
| |--Shiny Gold
|
|--Muted Yellow
At this point it's unclear if these relationships can form a loop - whether for example Muted Yellow could contain Light Red. If so, then this problem changes from a Tree to a directed graph, since the relationships are one-way only (foreshadowing foreshadowing). We'll only find out later once we load up all the rules and look at them in detail.
Parsing input
Since the input comes in the form of well-formatted text with with variable-width lines, this seems a perfect fit for a PEG parser, as described in Day 04. Using a PEG parser with a node visitor also lets us process each each node as it is being parsed, saving a loop or two. As usual, I will be using the parsimonious library for Python. Importing it with from parsimonious.grammar import Grammar
Let's construct the PEG grammar one part at a time. First let's consider this entry:
bright gray bags contain 2 bright gold bags, 5 dull lavender bags.
Let's split this into two parts, the PARENT part: bright gray bags contain and then a CHILDREN part: 2 bright gold bags, 5 dull lavender bags and then whatever's at the end of the line, a period and an optional newline character (it's optional because the last line in the document doesn't have one)
The PARENT part is easy to define, it's just:
- a COLOR which is always two words
- " bags contain " (with all the spaces
The PEG for just this is relatively simple
from parsimonious.grammar import Grammar
grammar = Grammar(r"""
PARETN = COLOR " bags contain "
COLOR = ~r"\w+ \w+"
""")
Testing:
print(grammar.parse("""bright gray bags contain """))
Output
<Node called "PARENT" matching "bright gray bags contain ">
<RegexNode called "COLOR" matching "bright gray">
<Node matching " bags contain ">
The CHILDREN part consists of one or more CHILD part, which can look like:
- starts with a NUMBER
- space
- a COLOR which is always two words
- space
- either
bagsingular orbagsplural - either
,or if at the end of the passage, we know the next character will be a.
So we can construct our PEG grammar accordingly:
grammar = Grammar(r"""
ENTRY = PARENT CHILDREN "." "\n"?
PARENT = COLOR " bags contain "
CHILDREN = CHILD+
CHILD = NUMBER " " COLOR " " BAGBAGS SEPARATOR
NUMBER = ~r"\d+"
COLOR = ~r"\w+ \w+"
BAGBAGS = ("bags" / "bag")
SEPARATOR = ~r"(, |(?=\.))"
""")
I've done a little weird thing with the separator, I've asked it to do (, |(?=\.)) which means "either , OR look-ahead for the . character but don't capture it". We don't want to capture the . character for the separator because we need it there to match the end of the ENTRY. This is known as a "positive lookahead" match in regex. I think the PEG could be written without one, but I've opted to use this to keep things a little simpler overall
I
Testing this on an example:
print(grammar.parse("""bright gray bags contain 2 bright gold bags, 5 dull lavender bags."""))
Output
<Node called "ENTRY" matching "bright gray bags contain 2 bright gold bags, 5 dull lavender bags.">
<Node called "PARENT" matching "bright gray bags contain ">
<RegexNode called "COLOR" matching "bright gray">
<Node matching " bags contain ">
<Node called "CHILDREN" matching "2 bright gold bags, 5 dull lavender bags">
<Node called "CHILD" matching "2 bright gold bags, ">
<RegexNode called "NUMBER" matching "2">
<Node matching " ">
<RegexNode called "COLOR" matching "bright gold">
<Node matching " ">
<Node called "BAGBAGS" matching "bags">
<Node matching "bags">
<RegexNode called "SEPARATOR" matching ", ">
<Node called "CHILD" matching "5 dull lavender bags">
<RegexNode called "NUMBER" matching "5">
<Node matching " ">
<RegexNode called "COLOR" matching "dull lavender">
<Node matching " ">
<Node called "BAGBAGS" matching "bags">
<Node matching "bags">
<RegexNode called "SEPARATOR" matching "">
<Node matching ".">
<Node matching "">
While this looks like a lot of text, most of it will be ignored. if we remove the lines that we won't actually do anything with, it would look like this:
<Node called "ENTRY">
<Node called "PARENT">
<RegexNode called "COLOR" matching "bright gray">
<Node called "CHILDREN">
<Node called "CHILD">
<RegexNode called "NUMBER" matching "2">
<RegexNode called "COLOR" matching "bright gold">
<Node called "CHILD">
<RegexNode called "NUMBER" matching "5">
<RegexNode called "COLOR" matching "dull lavender">
This is closer to the data we'll actually use.
One other thing we need to take care of, is that we also have a special case where there are no bags allowed inside
bright orange bags contain 5 dim bronze bags.
To do this, we'll add a special case of a TERMINAL, and raise the top level up by one to allow for a LINE to be either an ENTRY or a TERMINAL
LINE = (ENTRY / TERMINAL)
TERMINAL = PARENT "no other bags." "\n"?
ENTRY = PARENT CHILDREN "." "\n"?
Finally, unlike previously where we fed each entry separately into the PEG parser, this time we're going to have the PEG parser read the entire data file. So we need the parser to handle multiple entries. To do this, we have to add a new top-level pattern that says that a DOCUMENT can contain multiple LINE. The end result, our full PEG parser:
grammar = Grammar(r"""
DOCUMENT = LINE+
LINE = (ENTRY / TERMINAL)
TERMINAL = PARENT "no other bags." "\n"?
ENTRY = PARENT CHILDREN "." "\n"?
PARENT = COLOR " bags contain "
CHILDREN = CHILD+
CHILD = NUMBER " " COLOR " " BAGBAGS SEPARATOR
NUMBER = ~r"\d+"
COLOR = ~r"\w+ \w+"
BAGBAGS = ("bags" / "bag")
SEPARATOR = ~r"(, |(?=\.))"
""")
Now that we can parse the data, we'll be using parsimonious's NodeVisitor to traverse our parsed syntax tree to collect the information we need. I've explained some of this already in Day 04, so won't go into it too much. The code is:
class BagVisitor(NodeVisitor):
def visit_ENTRY(self, node, visited_children):
parent, children, *_ = visited_children
print("Entry", parent, "=>", children)
def visit_PARENT(self, node, visited_children):
return visited_children[0]
def visit_CHILD(self, node, visited_children):
return visited_children[2]
def visit_COLOR(self, node, visited_children):
return node.text
def generic_visit(self, node, visited_children):
return visited_children or node
bv = BagVisitor()
bv.grammar = grammar
The visit_COLOR() method is probably the core of our parser, its job is to deal with the COLOR node, and pull out the match and return it upwards to upstream nodes, which include PARENT, and CHILD, which then pass it upstream some more. By the time we get to visit_ENTRY() we have a nicely formatted COLOR values for parent and children.
The above puts a print() statemetn inside the visit_ENTRY(), so we can see each entry be successfully parsed. Running the example data:
bv.parse("""light red bags contain 1 bright white bag, 2 muted yellow bags.
dark orange bags contain 3 bright white bags, 4 muted yellow bags.
bright white bags contain 1 shiny gold bag.
muted yellow bags contain 2 shiny gold bags, 9 faded blue bags.
shiny gold bags contain 1 dark olive bag, 2 vibrant plum bags.
dark olive bags contain 3 faded blue bags, 4 dotted black bags.
vibrant plum bags contain 5 faded blue bags, 6 dotted black bags.
faded blue bags contain no other bags.
dotted black bags contain no other bags.""")
Output
Entry light red => ['bright white', 'muted yellow']
Entry dark orange => ['bright white', 'muted yellow']
Entry bright white => ['shiny gold']
Entry muted yellow => ['shiny gold', 'faded blue']
Entry shiny gold => ['dark olive', 'vibrant plum']
Entry dark olive => ['faded blue', 'dotted black']
Entry vibrant plum => ['faded blue', 'dotted black']
As can be seen, each entry has now been parsed into an easy-to-consume set of nodes. Note: TERMINAL nodes have been ignored, we actually don't need them.
Building the graph
To build the graph, we'll be using an extremely powerful network analysis package NetworkX. This is installed and imported with import networkx as nx.
The first thing we want to do is take a peek at what the data looks like to decide whether this data is in fact a Tree or a Graph. NetworkX is quite easy to use, to build a graph, you can simply, do the following to create a simple graph, and draw it:
graph = nx.Graph()
graph.add_node("A")
graph.add_node("B")
graph.add_edge("A", "B")
nx.draw(graph, with_labels=True)
NetworkX is smart enough to not create extra nodes if we try to use the same name, this makes our lives simple since we don't have to check whether the nodes exist. We add the add_node() and add_edge() functions to our NodeVisitor at the right places, and have it output a NetworkX graph as it parses:
class BagVisitor(NodeVisitor):
def parse(self, *args, **kwargs):
self.graph = nx.Graph()
super().parse(*args, **kwargs)
return self.graph
def visit_ENTRY(self, node, visited_children):
parent, children, *_ = visited_children
for child in children:
self.graph.add_edge(parent, child)
def visit_PARENT(self, node, visited_children):
return visited_children[0]
def visit_CHILD(self, node, visited_children):
return visited_children[2]
def visit_COLOR(self, node, visited_children):
self.graph.add_node(node.text)
return node.text
def generic_visit(self, node, visited_children):
return visited_children or node
bv = BagVisitor()
bv.grammar = grammar
This code now parses and returns a graph that can be analyzed! The usage is:
graph = bv.parse(input)
Let's draw the graph that comes out when we use the demo data is input:
pos = nx.nx_agraph.graphviz_layout(graph)
nx.draw(graph, pos=pos, with_labels=True)
Welp, clearly it's a graph and not a tree. So we need to switch our graph type to directed graphs, since we have clear parent-child relationship between nodes (a parent bag contains child bag relationship). This can simply done by switching nx.Graph() to nx.DiGraph() our edges are already all pointing in the right direction. This causes our diagram to get little arrows on the edges indicating the direction of the relationship.
Hang on, this is no good, let's give it some colours.
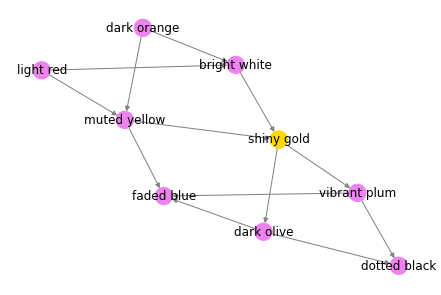
That's better. Remember this is still the example data given in the question, I'll plot our full graph in a sec.
Graph analysis
This part of the question basically boils down to "how many parents/grandparents/ancestors are there to the shiny gold bag?
To find this, we literally just ask NetworkX to give us our list of ancestors:
ancestors = list(nx.ancestors(graph, "shiny gold"))
Output
['bright white', 'light red', 'dark orange', 'muted yellow']
What are we doing here if we're not going to get fancy with the colors?
colors = []
for item in graph.nodes.keys():
if item == "shiny gold":
colors.append( "gold")
elif item in ancestors:
colors.append("chartreuse")
else:
colors.append("violet")
pos = nx.nx_agraph.graphviz_layout(graph)
nx.draw(graph, pos=pos, node_color=colors, edge_color="grey", with_labels=True)
Ok, let's do this for real now, with our real data:

Visualizations aside, grabbing len(ancestors) gives our answer to the question.
The Challenge Part 2
Part 2 is another traversal problem, but this time we must make use of the number of bags that can fit inside another bag, and multiply up, effectively counting the maximum number of bags possible if every bag contained its maximum complement of child bags.
Interestingly this tells us that there are no loops in the graph, because if there were, the number would be infinite. In other words, this directed graph is an acyclic one; a directed acyclic graph (DAG), which those of you working with data and CI pipelines might be familiar with.
So first we need to update our parser to save those scores with the edges. Our NodeVisitor becomes:
class BagVisitor(NodeVisitor):
def parse(self, *args, **kwargs):
self.graph = nx.DiGraph()
super().parse(*args, **kwargs)
return self.graph
def visit_ENTRY(self, node, visited_children):
parent, children, *_ = visited_children
for count, child in children:
self.graph.add_edge(parent, child, count=count)
def visit_PARENT(self, node, visited_children):
return visited_children[0]
def visit_CHILD(self, node, visited_children):
return (visited_children[0], visited_children[2])
def visit_COLOR(self, node, visited_children):
self.graph.add_node(node.text)
return node.text
def visit_NUMBER(self, node, visited_children):
return int(node.text)
def generic_visit(self, node, visited_children):
return visited_children or node
Now for the tricky part. Since while we know how many bags are inside any given bag, we don't know how many bags are inside THOSE bags until we go check. We have to recursively open up the bags all the way down to the bottom where there are bags containing no other bags, in order to multiply up the total number of bags. We have to write a recursive traversal function (it turns out to be depth-first). Unfortunately, NetworxX doesn't have any tools that'll just give us an answer, so we have to write our own recursive traversal with count multiplying:
def get_count(parent):
count = 0
for child in graph.neighbors(parent):
count += get_count(child) * graph.edges[parent, child]["count"]
return 1 + count
In other words: for each bag, get its children, and for each child, multiply how many of those child bags it has with how many more bags inside each child. Also don't forget to add one for the original bag itself.
This can be code-golfed a bit:
def get_count(parent):
return 1 + sum(get_count(child) * graph.edges[parent, child]["count"] for child in graph.neighbors(parent))
get_count("shiny gold") - 1
We have to subtract 1 at the end because the question wants how many bags shiny gold contains, without counting itself. The answer this gives is the answer the challenge wants.
A visualization of the edge with their numbers on the example data is:

I did also produce this visualization for the actual data, but there was so much going on, it wasn't much to look at. Running the full data and outputting the value of get_count("shiny gold") - 1 produces the result wanted by this part of today's challenge.
The full code to all parts of this challenge is:
from parsimonious.grammar import Grammar, NodeVisitor
import networkx as nx
grammar = Grammar(r"""
DOCUMENT = LINE+
LINE = (ENTRY / TERMINAL)
TERMINAL = PARENT "no other bags." "\n"?
ENTRY = PARENT CHILDREN "." "\n"?
PARENT = COLOR " bags contain "
CHILDREN = CHILD+
CHILD = NUMBER " " COLOR " " BAGBAGS SEPARATOR
NUMBER = ~r"\d+"
COLOR = ~r"\w+ \w+"
BAGBAGS = ("bags" / "bag")
SEPARATOR = ~r"(, |(?=\.))"
""")
class BagVisitor(NodeVisitor):
def parse(self, *args, **kwargs):
self.graph = nx.DiGraph()
super().parse(*args, **kwargs)
return self.graph
def visit_ENTRY(self, node, visited_children):
parent, children, *_ = visited_children
for count, child in children:
self.graph.add_edge(parent, child, count=count)
def visit_PARENT(self, node, visited_children):
return visited_children[0]
def visit_CHILD(self, node, visited_children):
return (visited_children[0], visited_children[2])
def visit_COLOR(self, node, visited_children):
self.graph.add_node(node.text)
return node.text
def visit_NUMBER(self, node, visited_children):
return int(node.text)
def generic_visit(self, node, visited_children):
return visited_children or node
bv = BagVisitor()
bv.grammar = grammar
graph = bv.parse(open("input.txt").read())
# Part 1
print("ancestor bags", len(nx.ancestors(graph, "shiny gold")))
# Part 2
def get_count(parent):
return 1 + sum(get_count(child) * graph.edges[parent, child]["count"] for child in graph.neighbors(parent))
print("total bags", get_count("shiny gold")-1)
Onwards!






Top comments (0)