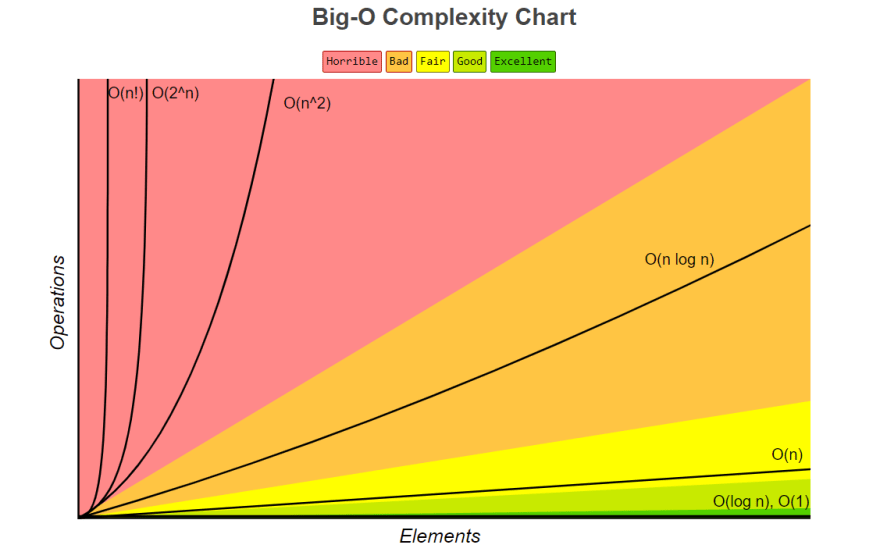
To demonstrate complexity, we use Big omega(Ω), Big Oh(O), Big theta(θ).
Big Oh(O) represents the worst case. Let's learn some of the basics for Big O notation.
O(n)
If a loop works for n times, the complexity is O(n)
#O(n)
def print_item(n):
for i in range(n):
print(i)
print_item(10)
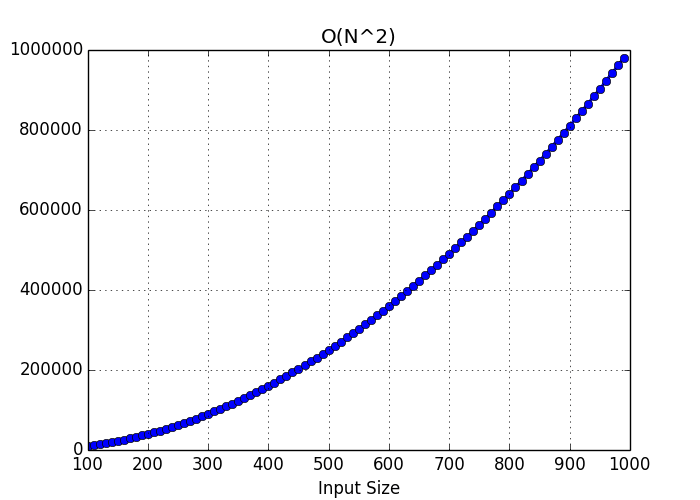
O(n^2)
If there is a loop within a loop, it is generally O(n^2). But here is a thing . O(n^3), O(n^100) or anything where n has more value than 2 , we will use n^2.
#O(n^2)
def print_item(n):
for i in range(n):
for j in range(n):
print(i,j)
print_item(10)
print('#Another example')
def print_another(n):
for i in range(n):
for j in range(n):
for k in range(n):
print(i,j,k)
print_another(10)
#This belongs to O(n^3) but what ever multiples by n, we will just use O(n^2).
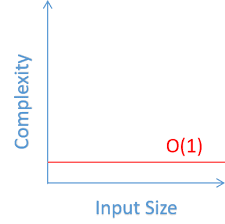
O(1)
If there is just one operation, we will have O(1).
#adding 2 numbers but just one simple summation . so , 1 operation
#O(1)
def add_items(n):
return print(n+n)
add_items(10)
#Summing 3 numbers but again it is one summation ; so 1 operation
#O(1)
def add_items1(n):
return print(n+n+n)
add_items1(10)
Drop Non dominants
If there is a less powerful complexity, we can drop that. For example, if we have O(n^2) and O(n) in a code, we can write it as O(n^2 + n) == O(n^2)
def print_item(n):
#O(n^2)
for i in range(n):
for j in range(n):
print(i,j)
#O(n)
for k in range(n):
print(k)
print_item(10)
#So, totally O(n^2 + n). But it will be O(n^2)
Drop Constant
We will ignore the constant on Big O notation.
def print_item(n):
for i in range(n):
print(i)
for j in range(n):
print(j)
print_item(10)
#here we have O(2n) but we will call it O(n).
here we have O(2n) and we won't write it as 2n. Rather as n.
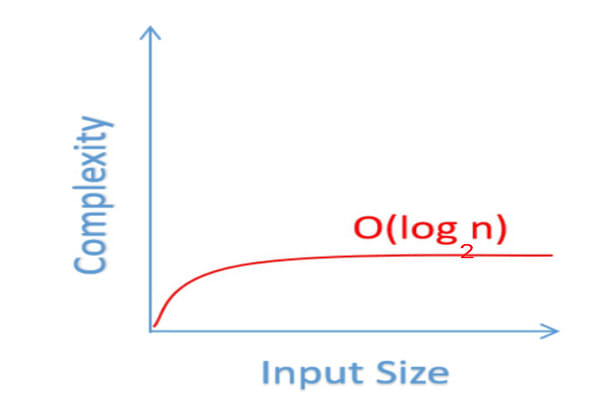
O(log n)
Assume that you have a sorted list of 8 numbers. Starting from 1,2,3,........8. You need to find 1.
So, you can use divide and conquer and first make 2 portion. First portion has 1,2,3,4 and second one has 5,6,7,8. Your desired number is on 1st portion and thus you will move to 1,2,3,4. now divide it to 2 portion and one has 1,2 and another has 3,4 . Remove 3,4 and now you will have 1,2. Now divide 1,2 and you have 1 and 2. You have got your desired 1. so , it took 3 steps or 3 equal distribution of 8 numbers to get your desired number.
Now, see that 2^3=8 . right? Which is like log2 8=3 . right? Thus it is log n notation.
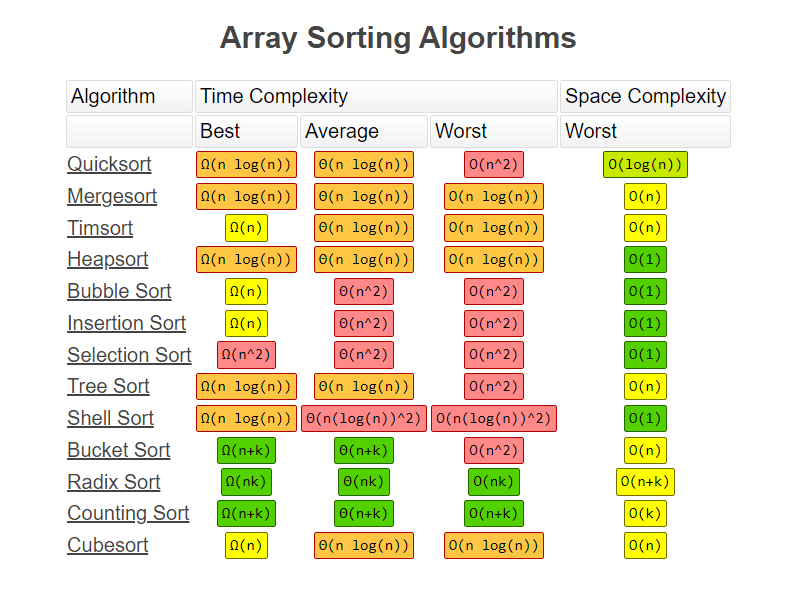
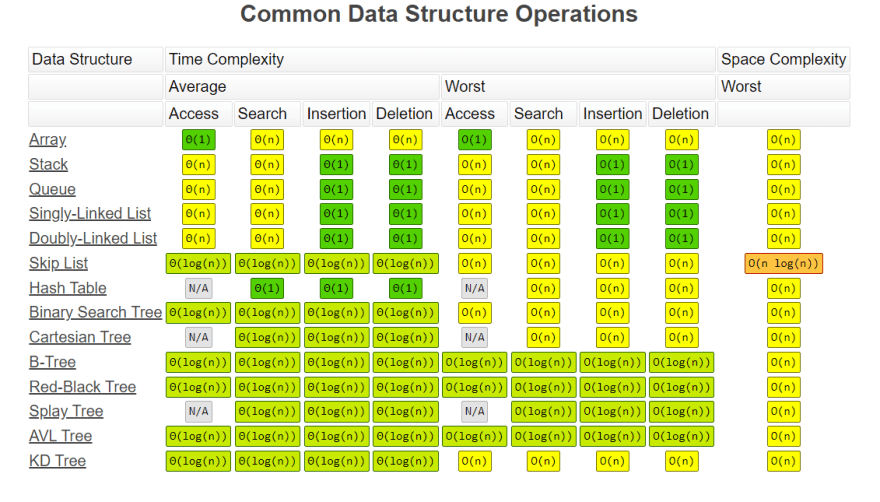
Check out this website to know about the complexity of certain algorithms:
https://www.bigocheatsheet.com/




Top comments (0)