3週間ほど経ち状況が変わってきていますが、感染症数理モデルの話を引き続き
SEIR モデルを JS で書く
新型コロナウィルスの専門家委員会から「基本再生産数 R0」や「実効再生産数 R」という言葉でてきます。他にも専門用語がでてきますが、これらを一般的に解説するかどうかの前に「その専門分野ではどのような使い方をされているのか?」を正確に把握するする必要があります。まあ、それが「専門分野」なのですから、同じ言葉を使っていても専門分野ごとに多少の違いはあるし、逆に同じ用語を他の分野でも同じ様に使っている場合もあります。どちらにせよ、その分野での専門用語の把握が必要です。
そんな訳で、2週間ほど前になりますが、SEIR モデルを Javascript で書きました。元の Python からそのまま JS に書き替えて、そのあと R0 を取り込めるようにしています。ちょっと、R0 の意味が分からなくてコードが間違えていたのですが、先日直したので、ここにコードの解説をしておきます。
SEIR モデルの数式
実は、Wikipedia を見ると、日本語のものと英語のものと SEIR モデルの式が若干違います。感染率 β の部分で総数 N が出てくるのですが、日本語の場合は、β(N) のように総数に依存するのですが、英語版のほうは β は N から独立しています。
感染率が総数 N に依存するのは変な感じがするので、英語版のほうを使うことにしました。
出生率 Λ と死亡率 μ は短期間なので、0 とみなせます。これを書き方えたのが下の式になります。
- N: 全体の総数
- S: 未感染者
- E: 潜伏期間中
- I: 発症者
- R: 回復者/免疫を得た人
になります。イギリスで発表された全国民が感染して免疫を得るという方式は、この SEIR モデルの、R になるということです。SEIR モデルの場合、感染して潜伏→発症→回復という順番になるのですが、かならず回復するというモデルなので、今回のような新型コロナウィルスのように発症後に死亡するケースがある場合には、致死率が2%程度だとしても相当の死亡者が予想されます。
即効撤回されたのは、良い判断でした。
この式の中でのパラメータとして、以下の3つがあります。
- α: 潜伏率
- β: 感染率
- γ: 回復率
これらは、潜伏期間 lp と発症期間 ip で書き替えることができます。
- α = 1/lp : 潜伏帰還の逆数
- γ = 1/ip : 発症期間の逆数
肝心の感染率 β の値ですが、基本再生産数 R0 との関係が以下のようになります。
死亡率 μ が 0 となるので、R0 は 感染率 β と 回復率 γ との比になります。
式の中では感染率 β を使うことになるので、次のように書き替えます。
この式から分かることは、
- 感染率 β と回復率 γ が等しいときに R0 が 1.0 になる
- 感染率 β が回復率 γ が大きいときに R0 は 1 を超えて、感染が拡大する
- 感染率 β が回復率 γ が小さいときに R0 は 1 より小さくなり、感染は縮小していく
という現象になります。これが専門家会議の言う「基本再生産数 R0」の意味です。
なので、できるだけ R0 < 1.0 の状態を保ちながら、ピークを低く抑えましょうという対策の根拠になります。
SEIR モデルを JS に直す
この数式を Javascript に直すと次のようになります。
v のところが配列になっているのは Python コードの名残りです。
function seir_eq(v,t,alpha,beta,gamma,N) {
S = v[0]
E = v[1]
I = v[2]
R = v[3]
ds = - beta * I / N * S // dS/dt = -βI/N*S
de = beta * I / N * S - alpha * E // dE/dt = βI/N*S-αE
di = alpha * E - gamma * I // dI/dt = αE - γI
dr = gamma * I // dR/dt = γI
return [ds,de,di,dr];
}
これを100日間繰り返すのが次の calc 関数です。
SEIR モデルに、試しに隔離率(T) を埋め込んでみて、発症者の一定割合を病院に隔離するというシミュレーションも入れておきます。
あと、S,E,I,R の数はマイナス値にはならないので繰り返し計算をするときに補正します。
function calc(state,alpha,beta,gamma) {
var t_max = 100 ;
var dt = 1 ;
lst = []
var N = Sinit + Einit + Iinit + Rinit
console.log( state );
for ( var i=0; i<t_max; i++ ) {
var d = seir_eq( state, i, alpha,beta,gamma, N )
var Si = state[0]+d[0]
var Ei = state[1]+d[1]
var Ii = state[2]+d[2]
var Ri = state[3]+d[3]
// 感染者を発見して隔離する
dx = Ii * T
Ii = Ii - dx
Ri = Ri + dx // 免疫者に加算
// マイナス値を調節する
if ( Si < 0 ) {
Ei = Ei + Si; Si = 0;
}
if ( Ei < 0 ) {
Ii = Ii + Ei; Ei = 0;
}
if ( Ii < 0 ) {
Ri = Ri + Ii; Ii = 0;
}
state = [ Si, Ei, Ii, Ri ]
// console.log( state );
lst.push( state );
}
}
グラフ化する
これに vue.js とグラフツールの c3.js を追加したが次の形です。
このグラフは基本再生産数 R0 が 10 のときのものです。10 というのは非常に多い値なのですが、いわゆるダイヤモンドプリンセス号のような閉鎖空間のクラスター(患者集団)の場合がこれに相当します。時間を追うごとに加速度的に感染者が広がります。
注目して欲しいのは、以下の3点です。
- 発病者のピークは感染スタートよりも左にある
- 潜伏期間中(黄色)のピークは、発病者(緑)のピークよりも左にある
- 最終的にほとんどの人が回復者(赤)となる
このグラフでは潜伏期間2週間で考えているので、発病者(緑)のピークは感染スタートから2週間以降になります。感染スタート時にすべての人が感染する訳ではないので、幅を取って2週間から3週間というところです。これが、現在の花見や春休みのシーズがスタートとなったときに、2,3週間後に流行するのでは?という理由です。
当然のことながら、発病期間のピークの前に、潜伏期間のピークがあります。SEIR モデルは潜伏期間中には罹患させないモデルになっていますが、新型コロナウィルスは潜伏期間中も罹患させる可能性がある、または無症状の場合も感染さえる場合があるという「可能性」が指摘されています。
このため、潜伏期間中の人が活発に活動すると、その後に発症のピークが出るかもしれません。
SEIR モデルの場合は、最終的にほとんどの人が感染して回復します。というか、無限に計算を続ければ100%の人が感染し回復して終わるようになっています。
先に書きましたが、SEIR モデルの場合は発症→回復となるので、死亡者がいません。実際の新型コロナウィルスでは死亡するので、最終的な回復者数×死亡率が全体の死亡数になってしまいます。
このため、無防備な策は誤りです。
基本再生産数 R0 を 1 に近づける
基本再生産数 R0(あるいは実効再生産数 R)は、感染率 β と回復率 γ との比率になります。
R0 を 1.0 に近づける(1.0以下にする)というのはどういうことかというと、数式からは以下の2つの手段があります。
- 感染率 β を下げる
- 回復率 γ を上げる
感染率を低く押さえるというとは、いわゆる「誰かに罹患させる確率を減らす」ということです。移動を減らすとか、3つの条件が重なる場所を作らないあるいは行かない、というのがその手段です。
もうひとつは、回復率を上げるというのは、病床を増やす、体力を蓄えておいて軽症で済ませるなどがあります。
基本再生産数 R0 を 10,5,2 と変化させてみましょう。
発症者(緑)のピークが限りなく右にずれることがわかります。
つまり「ピークを平らにする」ということは、基本再生産数 R0 を限りなく1.0に近づける(あるいは1.0以下にする)ことであり、同時に感染者のピークを限りなく未来に追いやることができます。
そして、新型コロナウィルスに対しての有効なワクチンや予防接種ができるまでの時間稼ぎができます。
基本再生産数 R0 が 1.0 のときは?
実験として、基本再生産数 R0 が 1.0 のときはどうなるのかを見ていきましょう。
感染者数(緑)のグラフが非常に平らになりほとんど直線になります。
罹患した後に回復した人も全然増えていないように見えますが、実際は回復者が100日目で25人になります。
これから分かることは、
- 感染がまったく広がらない訳ではない。わずかずつ感染は広がる
- しかし、対処可能な感染者数となる
ことを示しています。確率的に感染者は発生するのですから、何処から感染するかは分かりません。しかし、感染して発病したとしても、十分に治療可能な病床が用意できる、ことを意味しています。
github
コードは github moonmile/seir-model: SEIR model simulator に公開しています。
おまけ 実効再生産数 R とは?
ここからは私的なメモです。
基本再生産数 R0 と実効再生産数 R の違いを記述しておきます。
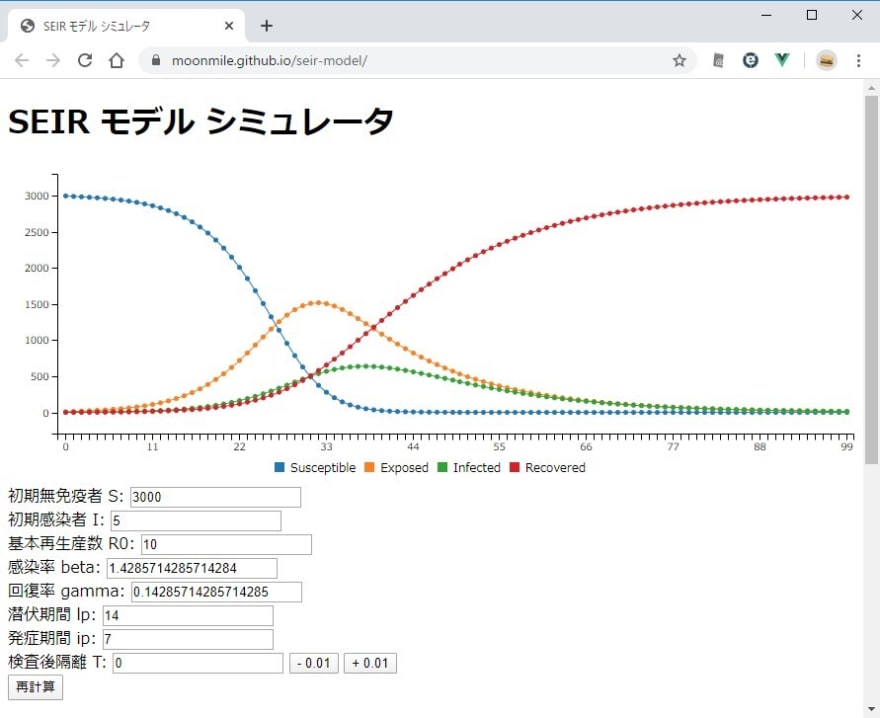
専門家会議では、最初の NHK での解説で「基本再生産数 R0」という用語を使っていました。再生産数という言葉から一般的に「基本再生産数を 1.0 以下に抑えれば、なにかグラフが平たくなる」ことが理解できたと思います。
このグラフが出たのが 2/24 の NHK です。
この感染症の流行モデルの元ネタは当時の NHK の解説では何処にも出てきませんが、専門家会議に北大の西浦教授がいることと、西浦教授の2017の論文から、SEIR モデルがベースであることがわかります。
そのあと、色々な批判もあったのち、海外でもこの「平たくする」図がでてくるようになりました。
ただし、これらの「ピークを平たくする」というイメージには、なんら数式的な根拠が示されていません。SEIR モデルを理解しているのか、それとも読者が SEIR モデルを理解できないと思っているのかは定かではないのですが、肝心の数理モデルはでてきません。twitter で #FlattenTheCurve というハッシュタグで拡散されつつありありますが、根拠は示されてません。
結果的に、発症時のピークを下げる=医療崩壊を防ぐことになるので、効果は同じだと思われるのですが、私が懸念するのは、
- ピークを下げた時期の概算が示されていない
- ピークを過ぎた後の発症数の裾野が、いつまで続くのか示されていない
のが問題だと思っています。
また、新型コロナウィルスの特徴として無症状な人が多いことから、新しい感染者を0人にすることはほぼ不可能です。天然痘のように全ての人にワクチンをうって撲滅しない限り 0 にはなりません。
同時に「クラスター対策」として言われるように、基本再生産数 R0 は状況によって大きく変わります。全体の平均として 1.0 以下におさえると、マクロの全体として発症者が押さえられるのは確かなのですが、個々の感染しやすい場所、あるいは感染しやすい季節や場所などのミクロの視点で見れば、基本再生産数は大きく変わり分布を持ちます。
このため「実効再生産数 R」として「実効」を付けて、基本再生産数 R0 になんらかのパラメータを掛けます。いわゆる事前条件を加味します。
どうやら疫学の場合の実効再生産数は、二次感染の平均を考慮するようです。このあたり、最近の専門家会議での解説をみると「実効再生産数 R」と区別されていることがわかります。
詳細は2020年3月19日付けの提言を読むとわかります。
- 基本再生産数(R0:すべての者が感受性を有する集団において1人の感染者が生み出した二次感染者数の平均値)
- 実効再生産数(感染症の流行が進行中の集団のある時刻における、1人の感染者が生み出した二次感染者数の平均値)
基本再生産数は、一般的な都市での感染率 → 都市機能を保ったまま低く保つ必要がある(一般的なイベントの開催、通勤や通学の正常化など)
実効再生産数は、感染してしまった都市での感染率 → 緊急で下げる必要がある(北海道の緊急事態宣言、ロックダウン、都市封鎖)
のように区別します。

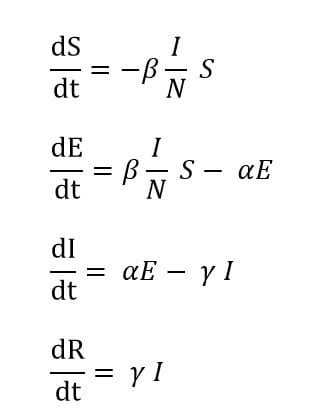








Top comments (0)