Pascal's triangle's beauty is in the complexities hidden behind its simplicity. It is a triangle that is constructed by summing the adjacent elements in preceding rows, and beyond this many elegant properties and challenges await.
For example, once such fact is that the sum of the nth row of Pascal's Triangle is given by .
One important thing to note is that the rows and columns run off of a 0-based index, similar to what we are accustomed to when dealing with arrays in programming.
Some important things to note
Each number on Pascal's triangle can be assigned a coordinate pair. An example of this is that, 20 occurs at . There is a neat formula we can use to find this number, called the binomial coefficient formula, stated as such for the coordinate where n is the row and k is the column:
The problem
How do we find the sum of a diagonal line on Pascal's triangle? The horizontal lines are as simple as , so is it that easy? Not quite. A quick way to solve this problem is to make more problems out of it, and the two that we shall tackle are the following:
- What is the nth term of the diagonal line k?
- What is the sum of the diagonal line k?
- BONUS: What is the sum of a cross of the diagonal lines k and -k?
Part 1: the nth term
An important observation to make before tackling this component of the problem is shown above. There is symmetry between the lines k and -k, this is outlined with the lines 2 and -2 above. This means that in our nth term formula, we must refer to k as |k| instead to persist this symmetry (as it will always be positive).
Let us solely work with the line k = 2 for now (ignoring the symmetrical k = -2). Below are the coordinates on this line drawn onto our triangle.
We can observe that all of our column coordinates = 2. If we are looking for the nth term, the row coordinate becomes n + 1. This means that any coordinate on this row is given by:
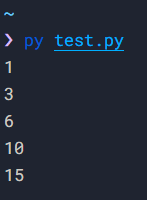
Which is our formula for the nth term of k = 2. Let us confirm this with the following code:
def secondRow(n):
return (pow(n, 2) + n) // 2
for i in range(5):
print(secondRow(i + 1))
For row k = 3, it is a similar story:
It is pretty simple to observe from here that for any diagonal line k, the nth term is given by
This neatly sums down to , which is the nth term of lines k and -k. Part one is solved.
Part 2: the sum of the kth row
We have done all of the heavy work in Part 1, this is where things become easy. To find the sum of the kth row, we must select an nth term to sum up until as these diagonals could theoretically go on forever. We can express this in summation notation and then sum this rather simply, as shown below:
Let's test this with some more code (:
import math
def nthTerm(k, n):
return math.factorial(n + abs(k) - 1) // (math.factorial(abs(k)) * math.factorial(n - 1))
def sumOfRow(k, n):
total = 0
for i in range(n):
total += nthTerm(k, i + 1)
return total
print(sumOfRow(2, 5))
We can independently verify that the sum of the first 5 terms of the second row is equal to 35 - our formula works!
[BONUS] Part 3: the sum of a cross
A cross is formed on Pascal's triangle between the lines k and -k. An example we have seen before is displayed below.
Due to this symmetry, finding this formula should be simple right? We just multiply our result by 2 as seen below:
This does work, however sometimes it will not. And this is when there is an intersection between the lines. This occurs when the inequality is true. So we must sometimes subtract the value of the intersection coordinate, but how can we find that? Look back upon our coordinate formula from earlier, and notice that the intersection coordinate is . This yields the following formula when this inequality is true:
All cases have been accounted for, so we can now safely confirm that the sum of a cross on Pascal's triangle is the piecewise function such that:
Conclusion
Even while asking more complicated questions and attempting more obfuscated problems, Pascal's triangle still manages to maintain this aura of beauty around it - one that drags us back time and time again to its complex beauty.
While all of this maths may be utter waffle that will likely never be used, as Seneca the Younger once said - "It is better, of course, to know useless things than to know nothing."


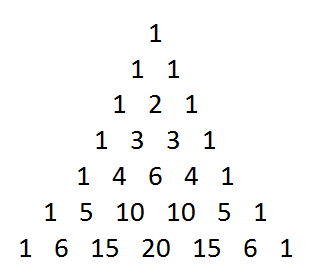



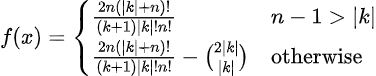


Top comments (0)