Table of contents
- Streaming and sketching algorithms
- Count Distinct problem
- Hyperloglog(HLL)
- HLL improvements
- Demo
Streaming and sketching algorithms
- Algorithms for data streams that examine data a few times and have low memory requirements.
- Storing individual elements is not possible in data streams as in most cases the size is enormous.
- We try to get approximate or "good enough" estimates while storing the "sketch" of the data(i.e some representation of data) but not the data itself. The "sketch" size should be much less than the data size.
- In short, we are doing a tradeoff between accuracy and memory.
Count Distinct problem
- Finding the number of unique/distinct elements in a multiset(set with repeated elements).
- e.g., unique visitors to a website and unique IP addresses through a router.
- Simple solution to this could be to keep a map of every element and its count. The main drawback of this approach is the storage of the map, as in the worst case, it is O(n).
- A sketching algorithm could prove helpful for this case as, in most cases, we would not care about 100% accuracy.
Hyperloglog(HLL)
Sketching algorithm designed to solve the count-distinct problem within acceptable error rate. Described in the paper "HyperLogLog: the analysis of near-optimal cardinality estimation algorithm", published by Flajolet, Fusy, Gandouet and Meunier in 2007. Improvements were proposed in "HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm", published by Stefan Heulem, Marc Nunkesse and Alexander Hall.
Based on simple obervation : On average, a sequence of k consecutive zeros in binary form of a number will occur once in every 2^k distinct entries. E.g. if we have a large enough collection of fixed-width numbers (e.g. 32/64/128 bit) and while going through it and we find a number starting with k consecutive zeros in binary form, we can be almost sure that there are at least 2^k numbers in that collection.
Simple Estimator
- To keep the input data uniform and evenly distributed we use a hash function. Now each entry is of fixed width(e.g 32/64/128 bits).
- While going through the collection we simply keep the count of longest consecutive sequence of zeros.
- Example of simple estimator (credits : engineering.fb.com) :
- We will define a counter/estimator as data structure which holds longest consecutive sequence of zeros for a collection ( R ).
- So, according to our theory this estimator will give estimate/cardinality as E = 2^R.
- Problem with this is that estimates will be only in powers of 2 and there can be lot of variability as only a single value having largest sequence of zeros can affect the total estimate.
Multiple estimators and HLL
To solve the issue faced by simple estimator we will use multiple estimators(let's say of m number) and divide the input collection between them. So, now each estimator has its own ( R ). We get single estimate using harmonic mean of individual estimates of counters.
A estimator is basically just a register or a single variable holding longest sequence of consecutive zeros. Each estimator can be thought of as a bin. So we have m bin i.e m registers (or just array of size m really) to imitate m estimator.
To divide the input collection between the m estimators we can reserve some starting bits of hashed value for bin index and rest bits for counting longest sequence of consecutive zeros.
Illustration of this (credits : engineering.fb.com) :
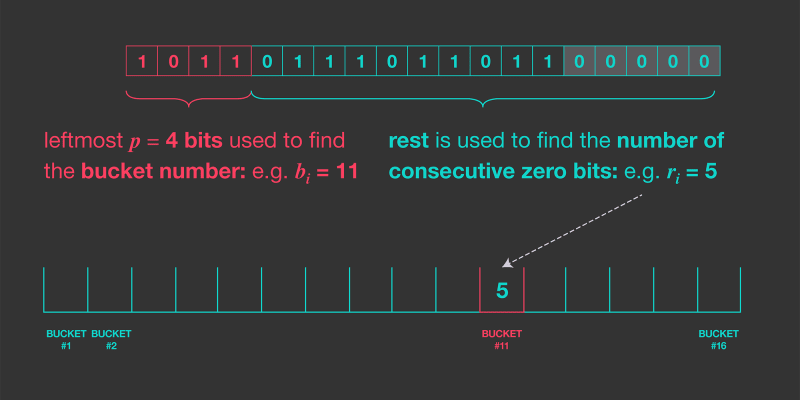
This is the basis of the hyperloglog algorithm. The algorithm described in the paper with some error corrections is as follows idea behind it remains same though :
HLL parameters and storage analysis
From above illustration we can clearely see that only 12 KB storage is required for a very large ndistinct value and relatively small error rate.
HLL improvements
Improvements were proposed in "HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm", published by Stefan Heulem, Marc Nunkesse and Alexander Hall :
- Using 64 bit hash function
- Estimating small cardinalities
- Sparse representation
64 bit hash function
Hash function with L bits will distinguish at most 2^L values. Beyond 4 billion unique entries 32 bit hash function wouldn't be
useful. 64 bit hash function would be usable till 1.8 * 10^19 cardinalities (which should suffice for all cases).
Here you can see size increased by just m bits or 2 KB(if m = 2^14 with error=0.008125).
Estimating small cardinalities
Raw estimate of original hll algorithm gives large error for small cardinalities. To reduce the error original algorithm uses linear counting for cardinalities less than 5*m/2.
Improvement paper found out that the error for small cardinalities is due to a bias(i.e algorithm overestimates the cardinalities). They also could correct the bias by precomputing the bias values and substracting them from the raw estimate.
This figure from Improvement paper shows the bias for raw estimate. Also, it shows linear counting is still better than bias-correction for smaller cardinalities.
From this they concluded to perform linear counting till 11500 for p = 14 and bias correction after that.
Sparse representation
When n << m, then most of the bins(2^14 if p=14) are empty and memory is wasted. So instead we can store just pairs of (idx, R) values (idx - index of bin, R - longest consecutive zeros sequence observed by that bin).
And when size of these pairs increases than the normal(dense) mode of m bins then we can convert to the normal(dense) mode. Thing to note is that we can merge pairs with same idx and keep just the pair with largest R.
Demo
For the demo I will be using postgress_hyperloglog. This is a postgreSQL extension implementing hyperloglog estimator. You can follow the installation steps from the repo README.
Example 1:
Here, we are generating 1,10000 series and then doing hyperloglog_distinct aggregate on these.
hyperloglog_distinct aggregate just creates a hll estimator, adds column elements and returns the estimate.
The hll estimates 9998.401034851891 which is pretty close to 10000 cardinality.
Example 2:
You can serialize these estimators, save them and load them again to operate on later.
hyperloglog_accum - creates hll estimator, adds column elements and returns the serialized estimator.
Output in second picture is actually base64 encoded byte string of the estimator.
Example 3:
We can also get estimate from this accumulated result(example 2).
Internal hll data structure is binary compatible with base64 encoded byte string - so they are interoperable. This way we can perform hyperloglog_get_estimate operation on the hll estimator returned by hyperloglog_accum.
For other examples you can refer to sql references and try it out yourself.
References :
- "HyperLogLog: the analysis of near-optimal cardinality estimation algorithm", published by Flajolet, Fusy, Gandouet and Meunier
- "HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm", published by Stefan Heulem, Marc Nunkesse and Alexander Hall
- https://engineering.fb.com/2018/12/13/data-infrastructure/hyperloglog/
- https://github.com/conversant/postgres_hyperloglog











Top comments (0)