Basics of Graph

Graph is data structure it has two componets

1. vertex / node
2. edge

Type of Graph

1. Undirect

degree(1) = 2 ← no of connected edges

degree(2) = 3

Total Number of edges in Undirect graph = 2 * E

(where E = Number of edges)

Path

sequence of node without reapeting or revisiting any node.

ex

1 3 2

1 5

❌1 3 2 3 → invalid can’t revisit

Undirected acyclic graph

1. Directed

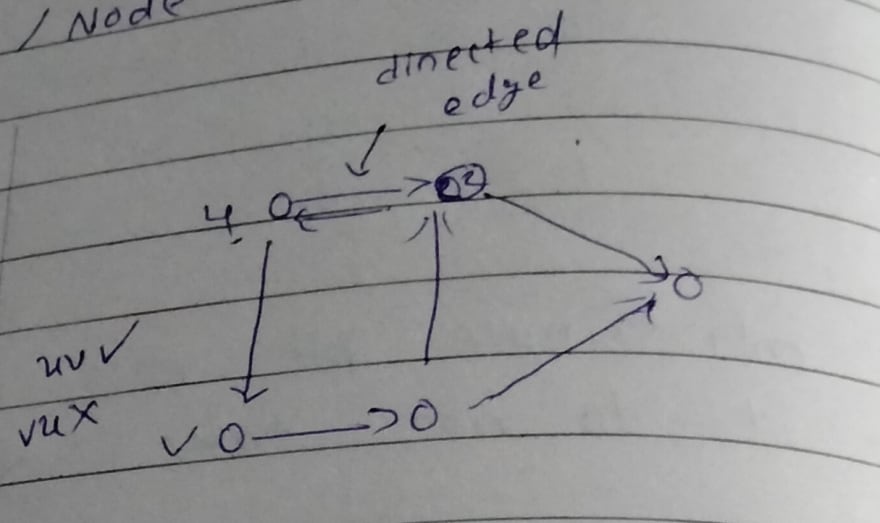
Indegree(2) = 2 ← number of incoming edges

Outdegree(2) = 2 ← number of outgoing edges

Path

• Qwe can move 1 to 5 and 5 to 4
• similarly 1 to 2 and 2 to 3
• but we can not move from 5 to 1

suppose if 2 to 1 is not there then we can call this Directed Acyclic Graph (DAG)

Representation of Graph

1. adjacency matrix

→ when two node are connected put 1 at their position

1. adjacency list

→ write name of name and name of other connected nodes

Example

Graph

Adjacency Matrix

Adjacency List

If edges are having some weights then

weighted undirected graph

if weight is not given if still you need then you can consider it as 1

weighted directed graph

Traversal in Graph

1. DFS - Depth First Search

→ Take one node and search all child until you reach leaf node still if dont find then comeback one step

1. BFS - Breadth First Search

→ First Search all childs then grandchild then again child of grand childs