This post was originally published on monades.roperzh.com
Transmitting digital data is tied to the risk of losing parts of it, just as a picture is exposed to scratches or sound is exposed to noise, digital information is susceptible to error, and while this risk can be arbitrarily decreased it always exists.
This article explores Error Correcting Codes, one of the methods used to mitigate data loss, along with a specific algorithm used for error correction called Reed-Solomon.
The explanations are focused only on the high-level concepts, leaving most of the mathematics aside.
Error Correcting Codes
Error Correcting Codes help receivers of a message to detect and correct damaged data. But how?
The fundamental idea is to add extra bits (called redundancy or parity) to the original data, that helps the receiver to detect and recover from errors. Encoding data with error correction doesn't mean that it can always be recovered, but adds an extra layer of safety.
One of the simpler ways to go about it's by repetition: append the original data three or more times. The receiver can compare this pieces of data and correct errors. In this specific case, the more you repeat the data, more chances you have to detect and correct an error.
While simple, the method of repeating data is not efficient. Something to remember when dealing with this kind of problems is the fact that in computing (like in life) it's all about compromises, you need to find a code that strikes the balance between the amount of data you send, the number of errors you can detect/correct, and the computational power needed to generate the parity bits. As you see, while the base idea is not complex, the problem gets tricky when defining the extra bits of data to add.
Enter Reed-Solomon
This idea of adding redundancy to the data opened the door to a world of different approaches to calculate it. Reed-Solomon (RS for short) is one particularly popular error correcting code: CDs, DVDs, Blu-ray Discs, QR Codes, and even satellites uses it.
RS codes became popular because they are relatively easy to encode/decode, and powerful. To give you a rough idea, typical RS configurations provide superior data durability and superior storage efficiency compared to the three-way replication described above with much less overhead.
The idea behind Reed-Solomon
Note: There's a considerable amount of mathematics involved in the process to generate RS codes, but this article focuses only on the concepts, letting to the reader the possibility to expand on the implementation details from any of the suggested resources.
RS bases it's underlying machinery in the concept that digital data is represented as binary numbers, therefore you can manipulate it arithmetically.
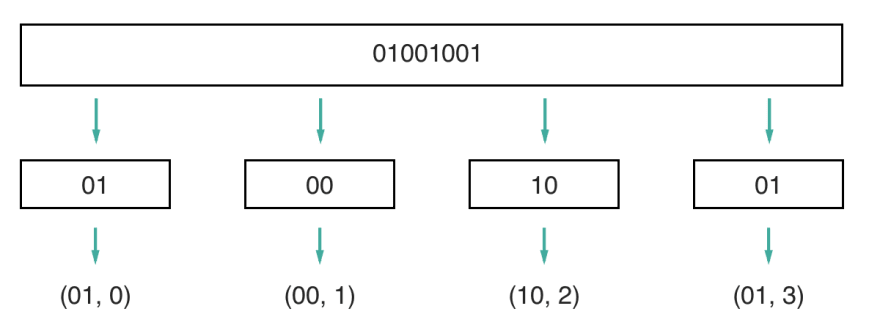
Think of the data to be transmitted as a long binary number, and imagine splitting this number into many numbers of arbitrary size. For example, you can split the number 01001001, into four chunks: 01, 00, 10, 01.
Now, if you assign to every chunk a number representing the order in which they appear in the original number, you end up with pairs:
At this point, it's important for you to fully understand what has just happened. The data has been split into pieces, and every piece got assigned an index.
And this is where the magic happens: think of this group of pairs as points of a polynomial, and indeed, you can mathematically find a polynomial that contains those points!
Since you have a polynomial, you are able to calculate an arbitrary number of points of it and store these points as the redundancy data. Then, if the original data points get lost/corrupted, the client can use this extra data points to reconstruct the polynomial and get the original data back!
Things get a lot more complicated when implementing them in actual code, but that's the base concept.
Based on that, you can play with two variables that affect the capacity to recover/detect errors.
The number of chunks in which you split the original data
As you increase the number of chunks, you get a polynomial that better represents your data, this comes with the cost of more computing to encode/decode the data.
The number of extra points you store
The more points you store, the more errors you can correct, but this comes with the cost of transmitting a bigger amount of data.
Suggested resources
There's a lot more about error codes and Reed-Solomon to be learned if you're interested here are some resources that I've found helpful:
- Codes: How to Protect Your Data - Michael Mitzenmacher
- Introduction to Reed-Solomon - Jeff Wendling
- Reed-Solomon Codes - Martyn Riley and Iain Richardson
- Engineering CS144 unit 7-4 - Stanford University
- An Introduction to Reed-Solomon Codes - Wicker and Bhargava





Top comments (0)