Some developers may be stuck on the concept of the "Big O" time complexity analysis. So you should read about how big-O work on this article.
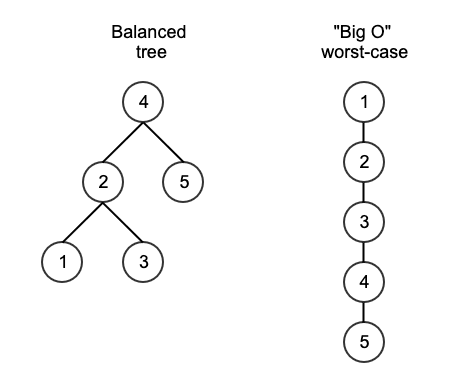
From the image above, you get the ideas of how a balanced tree looks like. "Big O" is about a problem in relation to the size of the input. In the diagram above, how was the shortest way to find the number 5? Obviously, the tree on the right takes more than the tree on the left.
1. Linear.O(n)
This is the most optimal algorithm that runs in linear time. No matter how much code you have and it stills run in the same linear time for every situation.
2. Constant. O(k)
Constant time algorithms have a running time independent of input size. Mathematical formulas, for instance, have fixed running times and are considered constant time.
3. Logarithmic. O(log(n))
Logarithmic is often seen on the trees. You can think about the height of the tree because it always includes traversing down the height of a tree and can be considered logarithmic in time.
4. Superlinear. O(n*log(n))
Most sort operation in O(n^2) time. Some of the popular sorting algorithms such as heapsort, mergesort, and quicksort. Usually, it is not a recommended way to do.
5. Quadratic or Cubic / Polynomial. O(n^2) or O(n^3)
Brute force algorithms often run in O(n^2) or O(n^3) because you are going to loop through all the situations. e.g. you want to find all the combinations of an array. [1,2,3] => [1,2,3], [1,3,2], [2,1,3] ... The complexity of the operation is n^3 time.
6. Exponential. O(2^n)
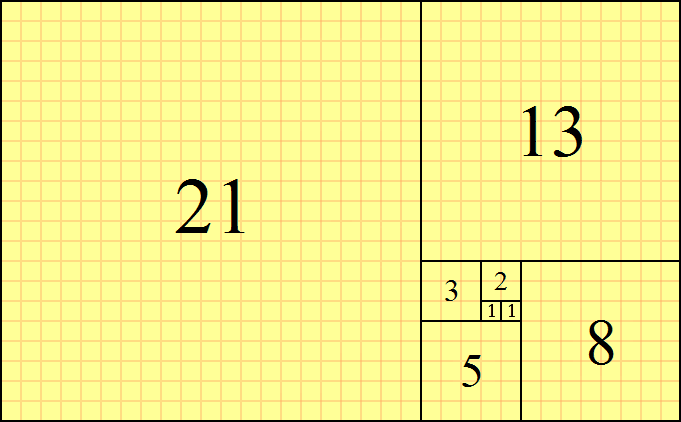
The exponential algorithm is also not the best but it is better than the factorial algorithm. One example is computing the fibonacci sequence. C(n) = C(n-1) + C(n-2). e.g. 1,1,2,3,5,8,13,21,34 ...
See the image below to understand factorial:
7. Factorial. O(n!)
This is the slowest algorithm that you never want to use. For example, list all the path of traveling n countries. Let's say you have three-country, the USA, Mexico, Canada. You first need to visit n city, and n-1 cities, and n-2 cities. The run-time stacks up as n*(n-1)*(n-2) = O(n!).
A lot of candidates get stuck here by either getting too deep in nitty-gritty details and overcomplicating this like saying "This is O(6 * k * n3), where k is the number of comparisons..." Most software engineers don't care about this level of detail, and you can often get away with simply saying "This is quadratic time because we have two for-loops, each one iterating from 1 to n."
One more tip - do not say "This is O(m + v + e)," when you haven't defined what m, v, or e are. You generally want to say "... where m is the height of the matrix, v is the number of vertices, e is the number of edges, etc.," Once you start reciting formulas without defining the constants you're using, your analysis will appear amateurish.


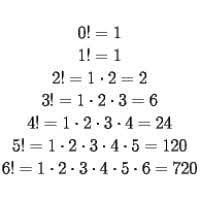

Top comments (0)