Bubble Sort Algorithm

1. Bubble Sort Technique
•Bubble Sort is the simplest of the sorting techniques.
•In the bubble sort technique, each of the elements in the list is compared to its adjacent element. Thus if there are n elements in list A, then A[0] is compared to A[1], A[1] is compared to A[2] and so on.
•After comparing if the first element is greater than the second, the two elements are swapped then.
•Using the bubble sort technique, sorting is done in passes or iteration. Thus at the end of each iteration, the largest element in the list bubbles up.

2. Complexity Analysis Of The Bubble Sort Algorithm
•In bubble sort, we make N-1 comparisons in the first pass, N-2 comparisons in the second pass and so on.

Hence the total number of comparisons in bubble sort is:
Sum = (N-1) + (N-2) + (N-3)+ … + 3 + 2 + 1
= N(N-1)/2
= O(n^2) => Time complexity of bubble sort technique
Thus the various complexities for bubble sort technique are given below:
Worst case time complexity O(n^2)
Best case time complexity O(n)
Average time complexity O(n^2)
Space complexity O(1)

Now , calculating total number of comparison required to sort the array
= (n-1) + (n-2) + (n-3) + . . . 2 + 1
= (n-1)(n-1+1)/2 {by using sum of N natural Number formula*}

=n (n-1)/2

For Worst case:
•Total number of swaps = Total number of comparison
•Total number of comparison (Worst case) = n(n-1)/2
•Total number of swaps (Worst case) = n(n-1)/2

Worst and Average Case Time Complexity: O(n^2).The worst case occurs when an array is reverse sorted.

For Best Case:
•The bubble sort technique requires only a single additional memory space for the temp variable to facilitate swapping.
•The space complexity for bubble sort algorithm is O (1).
Note that the best case time complexity for bubble sort technique will be when the list is already sorted and that will be O (n).

3. **Optimized Bubble Sort**
•To optimize our bubble sort algorithm, we can introduce a flag to monitor whether elements are getting swapped inside the inner for loop.
•In the inner for loop, we check whether swapping of elements is taking place or not, everytime.
•If for a particular iteration, no swapping took place, it means the array has been sorted and we can jump out of the for loop, instead of executing all the iterations.

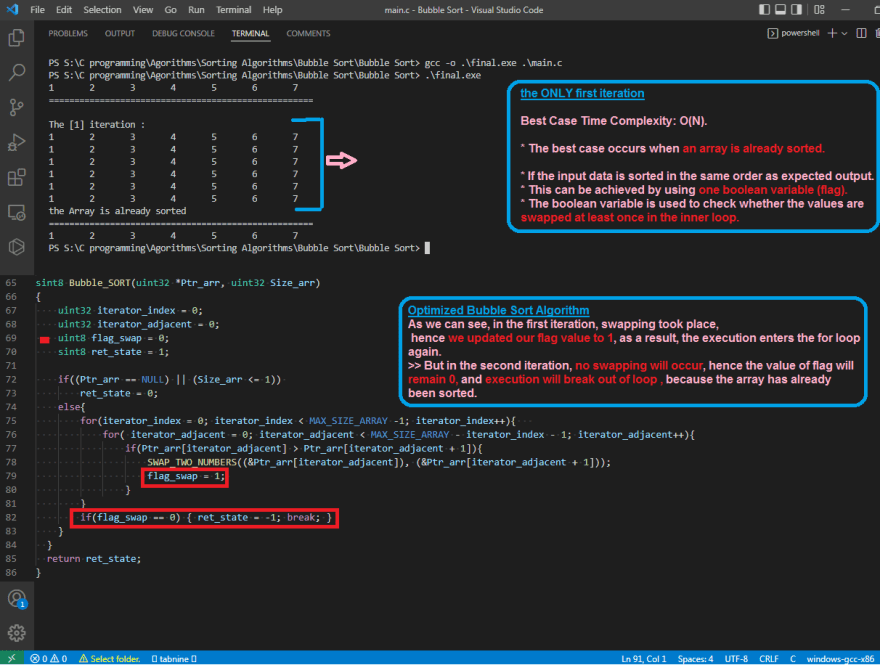
Let's consider an array with values {11, 17, 18, 26, 23}
Below, we have a pictorial representation of how the optimized bubble sort will sort the given array.

As we can see, in the first iteration, swapping took place, hence we updated our flag value to 1, as a result, the execution enters the for loop again.
But in the second iteration, no swapping will occur, hence the value of flag will remain 0, and execution will break out of loop.

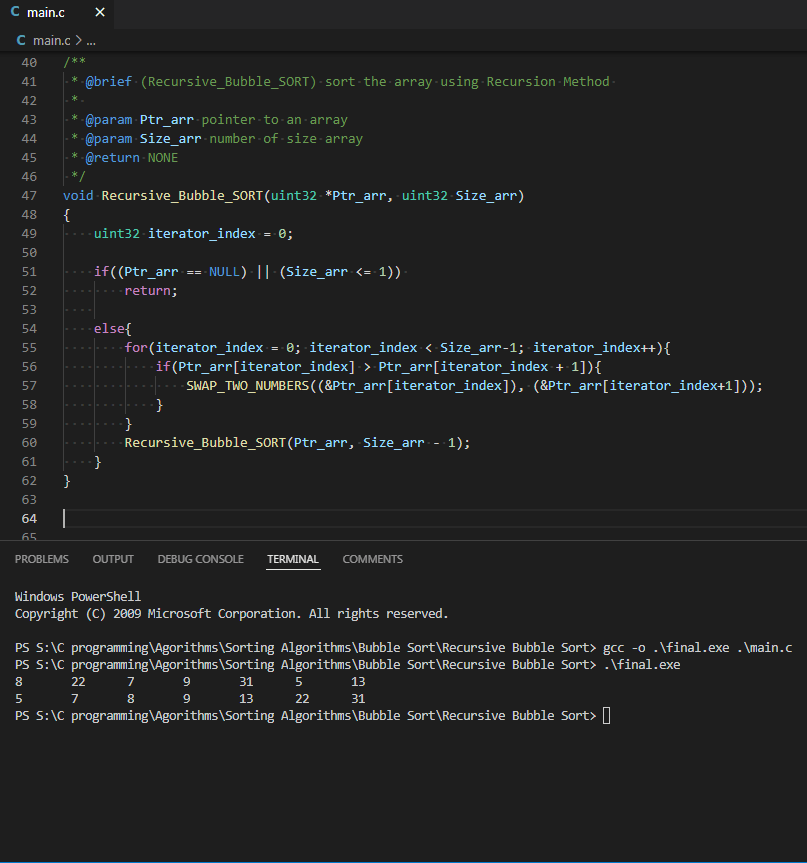
*4. Recursive Bubble sort *

•We will mimic the iterative approach of the bubble sort to implement it recursively.
•We will create a function for sorting in which we will check if the array length is 1 then return the array.
•Else loop till the given length and swap the elements depending on their order.
•Recursively call the same function again with one element less.

Time and Space complexity:
Time complexity: O(n^2).
Space complexity: O(n).
•We are calling the same function recursively for each element of the array and inside the function, we are looping till the given length of the array, So Time complexity is O(n ^ n) = O(n ^ 2).
•We are recursively calling the function for each element of the array, So space complexity is O(n).

5. Conclusion

•The main advantage of Bubble Sort is the simplicity of the algorithm.
•In bubble sort, with every pass / iterator, the largest element bubbles up to the end of the list if the array is sorted in ascending order.
•For the list to be sorted in descending order, the smallest element will be in its proper place at the end of every pass.
•Bubble sort is usually taken for introducing sorting to the audience.
•Bubble sort is also used in application like
Computer graphics wherein filling of polygon edges.
Require bubble sort to sort the vertices lining the polygon.

Does sorting happens in place in Bubble sort?
>> Yes, Bubble sort performs swapping of adjacent pairs without use of any major data structure. Hence Bubble sort algorithm is an in-place algorithm.

Is Bubble sort algorithm stable?
>> Yes, bubble sort algorithm is stable.

Where is Bubble sort algorithm used?
>> Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm.

In computer graphics, it is popular for its capability to detect a very small error (like a swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n).

The source Code is on My Github
•Bubble Sort: [((https://github.com/SohaibDar61/Algorithms/tree/main/Sorting%20Algorithms/Bubble%20Sort)]

•More Articles : [(https://www.linkedin.com/in/sohaibdar61)
•E-mail: [e-mail]
•Phone:[phone]
•Upwork: [(https://www.upwork.com/freelancers/~019e71f2adc499c4e8)]
•LinkedIn: [(https://www.linkedin.com/in/sohaibdar61)]

Anyone can edit or optimize the code , and I hope that revision helps and gets better.

Thank You.
Sohaib