Understanding Binary Search in JAVA

Why we need a searching algorithm in the first place 🤔?

Search algorithms are like helpful detectives for computers. They help computers find things quickly and accurately in a big pile of information. This is important because it saves time and makes sure we get the right answers.

Imagine searching for a specific toy in a messy room. A search algorithm is like a smart friend who knows exactly where to look, so you find the toy faster. These algorithms are used in many places, like when you search for stuff on the internet or when your GPS finds the best route for you. They're like superhelpers for computers!

Binary search

Some of us think,linear search is a basic technique. In this technique, the array is traversed sequentially and each element is compared to the key until the key is found or the end of the array is reached.

Linear search is used rarely in practical applications. Binary search is the most frequently used technique as it is much faster than a linear search.

you might be wondering what i mean by it's fast! there is a thing in coding called time complexity

O(n),O(n^2),O(nlogn),O(logn) and O(1)
where O(1) is the efficient time complexity.

Java provides three ways to perform a binary search:

1. Using the iterative approach
2. Using a recursive approach
3. Using Arrays.binarySearch () method

In this blog we are going to see iterative approach and remaining in the following blogs.

Iterative Binary Search:

In the binary search method, the collection is repeatedly divided into half and the key element is searched in the left or right half of the collection depending on whether the key is less than or greater than the mid element of the collection.

A simple Binary Search Algorithm is as follows:

1. Calculate the mid element of the collection.
2. Compare the key items with the mid element.
3. If key = middle element, then we return the mid index position for the key found.
4. Else If key > mid element, then the key lies in the right half of the collection. Thus repeat steps 1 to 3 on the lower (right) half of the collection.
5. Else key < mid element, then the key is in the upper half of the collection. Hence you need to repeat the binary search in the upper half

As you can see from the above steps, in Binary search, half the elements in the collection are ignored just after the first comparison.

Note that the same sequence of steps holds for iterative as well as recursive binary search.

Let’s illustrate the binary search algorithm using an example.

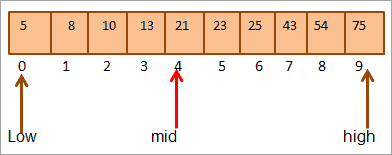
*For example, take the following sorted array of 10 elements.
*

Let’s calculate the middle location of the array.

Mid = 0+9/2 = 4

1) Key = 21

First, we will compare the key value with the [mid] element and we find that the element value at mid = 21.

Thus we find that key = [mid]. Hence the key is found at position 4 in the array.

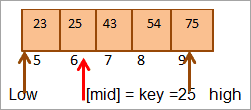
2) Key = 25

We first compare the key value to mid. As (21 < 25), we will directly search for the key in the upper half of the array.

Now again we will find the mid for the upper half of the array.

Mid = 4+9/2 = 6

The value at location [mid] = 25

Now we compare the key element with the mid element. So (25 == 25), hence we have found the key at location [mid] = 6.

Thus we repeatedly divide the array and by comparing the key element with the mid, we decide in which half to search for the key. Binary search is more efficient in terms of time and correctness and is a lot faster too.

Binary Search Implementation Java

import java.util.*;
class Main{  
 public static void main(String args[]){  
    int numArray[] = {5,10,15,20,25,30,35}; 
    System.out.println("The input array: " + Arrays.toString(numArray));
    //key to be searched
    int key = 20;
    System.out.println("\nKey to be searched=" + key);
    //set first to first index
    int first = 0;
    //set last to last elements in array
    int last=numArray.length-1; 
    //calculate mid of the array
    int mid = (first + last)/2;  
    //while first and last do not overlap
    while( first <= last ){  
        //if the mid < key, then key to be searched is in the first half of array
        if ( numArray[mid] < key ){  
            first = mid + 1;     
        }else if ( numArray[mid] == key ){ 
            //if key = element at mid, then print the location
            System.out.println("Element is found at index: " + mid);  
            break;  
        }else{  
            //the key is to be searched in the second half of the array
            last = mid - 1;  
        }  
        mid = (first + last)/2;  
   }  
   //if first and last overlap, then key is not present in the array
   if ( first > last ){  
      System.out.println("Element is not found!");  
   }       
 }  
}  

Output:

The input array: [5, 10, 15, 20, 25, 30, 35]
Key to be searched=20
Element is found at index: 3

The above program shows an iterative approach of Binary search. Initially, an array is declared, then a key to be searched is defined.

After calculating the mid of the array, the key is compared to the mid element. Then depending on whether the key is less than or greater than the key, the key is searched in the lower or upper half of the array respectively.

Hope this helped alot..! happy coding guys..!♥️