Think recursively...

What is Recursion:

- An act of a function calling itself.

For example, below is the pseudo-code to show how recursion works. The function called recursion is being executed twice, first in the global scope, then secondly, within itself. The function can then be called however the user chooses.

According to the Church-Turing hypothesis, any function that can be computed iteratively, can be computed recursively and vice versa (loosely translated). This function can take two cases.

1. A base case - to end the recursion
2. An iterative case - continues the recursion

A recursive function will call itself until the base case breaks the call. In this case the base for the below recursive function is

if (num <= 0)

This function will return 0 as the answer. It will continue to call itself recursively, decrementing by 1 (num -1) for every call. For each call num will take values of 5, 4, 3, 2, 1 until the base case of num = 0 hits, which will then trigger the return 0.

Taking a simple function that adds elements of an array: let array = [3,2,3,6,5]. The problem can be solved quite easily with a for loop. Looping through the elements of the array and adding to each element. However, we also know from the Church-Turing hypothesis, that we can also execute the same recursively.

A for-loop sum function below:

The recursive sum function is below:

The recursive sum function is shorter, than using the for-loop. This is usually the case even for more complex functions. The base case for the recursive function is if (arr.length > 0). This function will call itself as long as the length of the array is not 0. Once this length becomes 0, it executes the return.

To understand exactly what is happening, we will need to employ the services of our old friend,
console.log() with a more robust example of arithmetic mean. This is what is commonly referred to an an average.

This function increases the count as the function calls itself repeatedly. This is quite useful in many ways. One, we can know how many times the recursion occurred. However, since The size of the array also reduces with each call, arr.length also changes. This means if we try to simply return init / arr.length, we will be dividing by 0 as arr.length reduces to 0. Why is that? You guessed, it, the use of the arr.slice(1). The slice method, in this case, removes the first element from the array and returns a new reduced array on every recursive call.

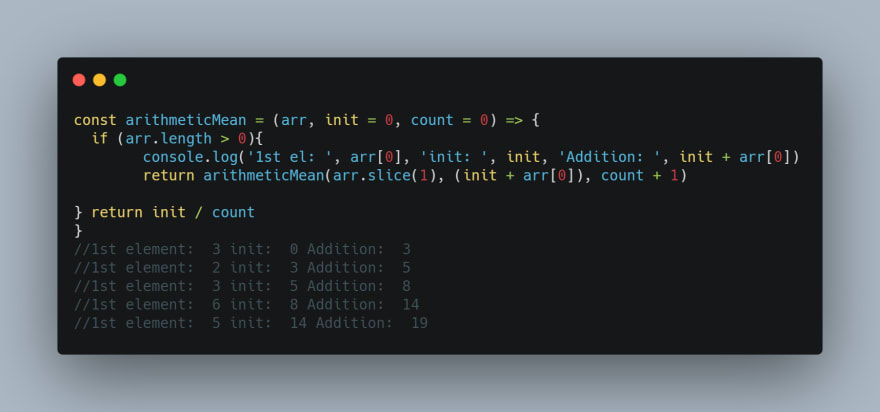
Hence increasing the count is handy as the count can be used in place of arr.length as it increments to the size of the original array. The init argument is where the magic happens. Since the initial value of init = 0 at the start, it is updated through arr[0] + init. This means a new value of init will have the first element of the array added to it on every call, ensuring that when the base case has been met, all the init contains the sum of all the elements of the array. Now, when we return init, we are simply returning the sum of the elements of the array. Also, because count + 1 ensures the count increases from the declaration value count = 0, it increases by 1 on every recursive call, ultimately matching the length of the array, hence we can simply do return init / count will give us the sum of the elements divided by the number of elements within the array, which is the arithmetic mean.

Note the formulae of arithmetic mean, geometric mean and harmonic mean is below for referrence.

I try to challenge myself to change functions written using for loop to recursion. This is so I can challenge myself to understand what happens each time a function is called. Notice that everything within the recursive function will update on each call. The same logic can be followed for geometric and harmonic mean. Doing trivial exercises helps one understand the mechanics of the code, for loops are easy to follow, recursion isn't as clear-cut as loops, but setting a count so you know how many times the function was called helps mentally map what is happening.

I hope this helps you as much as it helped me. Below are the codes for both geometric and harmonic mean. Note that init = 1 and not init = 0. Happy recursions.