Originally posted here
It’ll be a tough task to find somebody in 2019, who hasn’t heard about serverless computing. AWS Lambda, GCF and Azure Functions — we all know what these things mean. Cost saving infrastructures, infinite scalability, no operations, no sys admins — how cool is that? We read a lot of case studies by large companies, which claim that they managed to reduce their cloud computing costs X times simply by switching to AWS Lambda or any other cloud market FaaS solution. But, as we know, there are no silver bullets in software engineering world, there are only suitable per particular problem trade-offs.
Let’s consider AWS, for example. While we are truly abstracted away from any server administration with Lambdas, we feel great. But once we realize that for some particular reason we might need to put our function in a VPC (e.g. lambdas need to talk to RDS, ElastiCache or simply anything without a public IP/DNS name), with the first cold start we realize that we’re screwed. Yeah, it is a problem to start a Lambda in a VPC. I won’t go far in details, you can read a lot about it VPC cold start problems on AWS official docs. Long story short, functions have to be associated with ENI to be able to talk to instances in VPC, and ENI allocation can take up to 10 seconds, which means that cold start of any function within a VPC will most likely take more than 10 seconds! How cool is that? Not really.
Anyhow, VPC cold start is not the only problem we should think about. This problem affects performance and latency of our apps, but there’s something more behind it. If we put our Lambdas in VPCs, we have to keep in mind IP capacity of its subnets. Details can be found here, but simply speaking, it is possible for a VPC to run out of free IP addresses in case of very high number of concurrent requests coming in. For this particular reason, AWS provides us with this famous and simple formula to calculate ENI capacity:
ENI Capacity = Projected peak concurrent executions * (Lambda RAM in GB / 3GB)
Given a CIDR block (e.g. 10.0.0.0/24) and RAM, that we allocate for a Lambda function, we can estimate, how many concurrent requests the subnet will be able to handle, which can be very useful, when we design our subnets and distribute IP addresses.
However, I tried to go one step forward and tried to make use of Little’s law for distributed systems. This law provides us with such formula:
If we take lambda symbol as an amount of requests per second and W as an average time for each request to complete, L will stand for the mean number of concurrent requests that we’re going to have within a system in any moment of time. Let’s have an example of a shop. Let’s say that people arrive in the shop at the rate of 10 per hour and spend there half an hour. So the average number of people that we’re gonna have in the shop in any moment of time will be equal to 10 x 0.5 = 5. Very simple.
Little’s law is widely used in estimation of distributed systems’ throughput. However, it gives us a mean value, which is not actually suitable for precise estimation, because it doesn’t consider real world side effects. System’s latency (W) tends to change over time, due to resource allocations, network problems or simply anything else. Mark Brooker (lead engineer in AWS Lambda team) has a nice blog post about it, where he describes the way we can make use of Little’s law closer to the real world.
However, even though the law doesn’t give us a precise estimation, we are still able to make use of it for some cases. For example, we actually can easily calculate the amount of IP addresses in a VPC, so that it will be able to handle a required requests per second rate.
Let’s say that there is requirement for a system, built on top of Lambda in a VPC, to be able to handle 1000 requests per second. We need to make sure that we have enough of IP addresses in our subnets to fulfill the requirement. So let’s do some simple math!
First of all, we need to find out how much time the code in lambda requires to run and how much RAM it consumes, so that we can set a proper amount of memory for our function. It is easy to do that with CloudWatch logs, where AWS provides us with duration in milliseconds and used memory in megabytes. For example, we found out that average duration and memory consumption are 500ms and 128 MBs accordingly. Keeping in mind the VPC cold start we can easily add 10 seconds to the duration and the result will be W in Little’s law. Now we can calculate L:
L = 1000 (req/s) * (10 + 0.5) (s)
L = 10500 (req)
This number shows us that during VPC cold start we’re going to have at least 10500 concurrent lambda functions running. Now we need to calculate the necessary amount of IP addresses. In the formula, which AWS provided us to calculate ENI capacity, we can substitute L as projected peak concurrent executions and 128 MB (0.125 GB) as Lambda RAM:
ENI = 10500 * (0.125 / 3)
ENI = 4375
As we can see, 4375 IP addresses will be enough to make sure that we’re good. The closest CIDR block to fulfill this requirement will be 10.0.0.0/19, which is 8192 (8187 actually, since AWS claims to reserve 5 addresses for internal needs). 10.0.0.0/20 will give us 4096 (4091), which a little less than we need.
Still, it’s not quite precise. In most cases Lambdas are in a VPC, because they need to connect to, let’s say, RDS. This means that they are going to open database connections and it will surely downgrade database performance a lot, which will reflect on W in Little’s law. You may find the mentioned Mark Boozer’s blog post very useful, where he goes beyond raw Little’s law.
Important note
Of course I have to say that during Re:Invent 2018 AWS announced a solution for VPC cold starts with some fancy remote NATs. Most likely in close future we won’t need to calculate IP addresses and have these 10 seconds delays anymore, which is awesome.
Looks like @awscloud has some ideas to fix #Lambda cold starts in a #VPC. 🙌 Coming in 2019! #serverless #reInvent22:36 PM - 29 Nov 2018
60
146
But I just found it interesting enough to write about. Thanks for your attention!
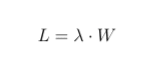
Top comments (1)
10500 * (0.125 / 3) is not 4375. It is 437.5. What gives?