Gini Splitting Criterion

Gini index was originally developed by statistician Corrado Gini and was used to measure economic inequality. As discussed in the previous post, Gini index is one of the options for a cost function in Sklearn Decision Trees.
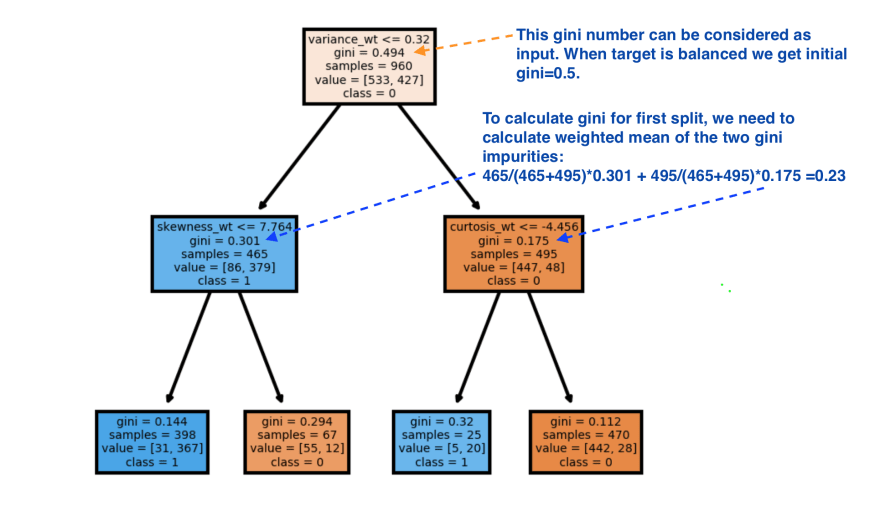
Gini impurity index varies between 0 and 1. A low value represents a better split within the tree. If we calculate the Gini index with the balanced binary target, then the initial Gini (before any split) is 0.5.

Gini index for a multiclass problem, where p is the frequency of each class, n is the number of classes:

Here I will do an example with binary classification and Gini simplifies as:

where p+q =1.

So, when we design the split in the tree, in most of the cases, two nodes will have two different Gini indices. To describe the quality(or purity) of each split, we can use the weighted mean of two Gini indices. This is the idea behind decision tree algorithms with Gini criterion.

Let's play with scikit learn Decision Tree Classifier using Banknote authentication Data Set.

Here I used 960 rows as a train dataset:

I constructed a simple tree with depth = 2. Gini index for each split can be calculated manually by applying formula.