In this post, I would like to show briefly how theoretical components given in the gradient boost for classification are implemented in sklearn.
Gradient Boosting Classifier uses regressor trees. Meaning, we use mean squared error as splitting criteria and differentiable Loss function (Log - Loss by default). I guess the name of the regressor tree here comes from the Logistic regression Log-Loss function.
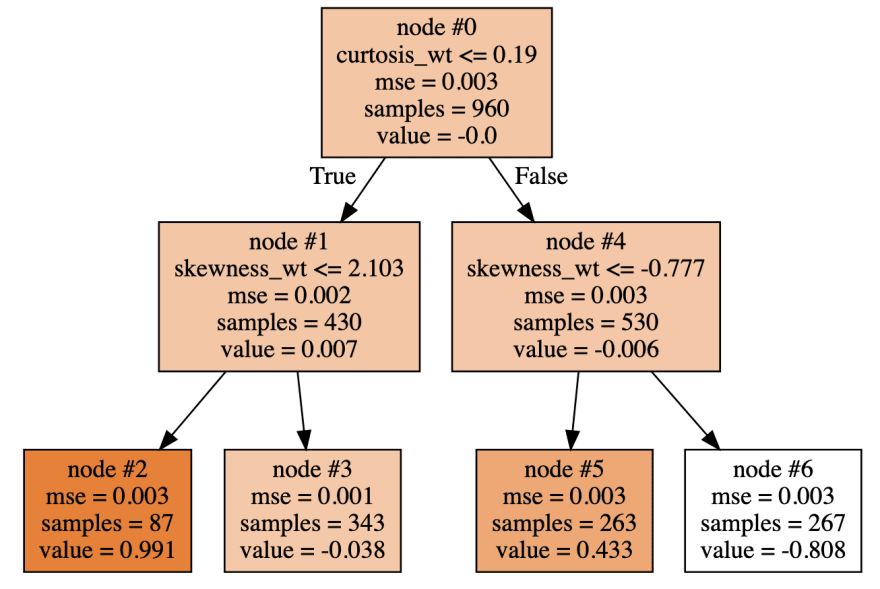
Let us see the first and last tree in the model (repo reference).
As we can see by iteratively building and fitting trees to the negative gradients of the Log-Loss Function (-G=Residuals =True_Probability - Predicted_Probability), each leaf gives an output value.
Each ouput value is calculated like
predicted_leaf_output = (sum of residuals in the leaf) / [sum of the (Predicted_Probability*(1-Predicted_Probability)].
Then using log of odds, we can convert it to the new probability:
log(new_odds) =log(previos_odds) + alpha * output_value
New_probability = e^log(new_odds)/[1+e^log(new_odds)].
Then we just use a loop to keep iteratively improve our prediction till we reach the maximum number of estimators or specified hyperparameters in the classifier.
When we need to predict for a new data, this data (number of known features with unknown label) will go through that trained model (n number of fitted trees), and using the above formula probability will be calculated and Class 0 or 1 assigned respectively for binary classification.




Top comments (0)