Machine Learning Guide

Machine Learning Guide

Basics

Quick Info

Audience:

This guide is made for beginners with basic knowledge in Python programming.

Goal:

Predict house sale prices in a Kaggle beginner competition (predicting house sale price) using machine learning libraries in Python.

Resources:

Kaggle:

House Prices - Advanced Regression Techniques

Python Script (Main):

KagglC1.py

Python Script (Supplement):

KagglDataC1.py

PDF version of this guide:

Machine_Learning_Blog.pdf

Last Edit:

2025 March 25

Credits:

This guide is inspired by chapter 2 in Hands on Machine Learning by Aurélien Geron. I am in no way associated with the author himself. This guide does not replicate any parts of the book, and the code presented here is based on publicly available source codes.

Introduction

I want to use this introduction briefly to explain how to learn the basics of machine learning, because it can be quite intimidating for newcomers with little background knowledge. Since we will require Python, you should get familiar with the most basic concepts (variables, lists, tuples, dictionaries, functions, loops, if-else-statements). You will also encounter other concepts like lambda functions or classes, but our use cases are rather simple. Everything else can be learned on the fly. You will probably find out that learning Python libraries for machine learning or data science almost feels like learning a new language, anyway.

For now you do not need much mathematical background except very simple school mathematics. Of course more advanced topics require more knowledge (like basic linear algebra or probability theory), but as long as you do not intend to build your own machine learning tools, you can simply use the existing ones without knowing every mathematical or technical detail working under the hood.

The best way to get a grasp on machine learning is to start with very practical books like Hands on Machine Learning by Aurélien Geron, because they explain working source codes for real world examples. The alternative would be starting from scratch with very basic books, but you may not have time to learn every detail right from the beginning.

Of course practical books can have a very steep learning curve, but if you use learning techniques like priming, incubation, and the 24-hour rule combined with practical coding you can get started with machine learning within just a few days or weeks. This means that you do should not try to memorize everything from the beginning, but rather skim through the working examples, and revisit the details later on, while experimenting with parts of the code. The more you repeat the first-skim-then-revisit-cycle the better you will get without wasting too much time on less important details.

One way to soften the steep learning curve is to start with crash courses like this one. So without further ado, let us begin.

Installation

In order to run the Python code you only need a webbrowser, if you use Google's Colab. Btw. Aurélien Geron's source code used in his book is also publicly available on Colab, even though it may not be very beginner friendly.

However, I recommend running everything locally on your computer for the ease of use. We will be using Visual Code, which has a lot of nice comfort functions that are probably not available on Colab. The only downside is that the initial installation takes a bit of effort and about 10 GB space in total.

First you can install Visual Code and the Jupyter extension. Jupyter allows you to run certain parts of your code in any order you like. We will refer to these code parts as Jupyter cells.

All you need to do is create a Python script file with the .py ending, and open it in Visual Code. Each cell is separated by #%% at the beginning of each line. If you want to see how it works, you can experiment with the following simple code.

#%%

x = 3

#%%
print(x)

#%%
del x

Algorithm 1: Jupyter Cell

Next you need to install the Python libraries required for the basic machine learning tools. Instead of downloading them separately, you can install Anaconda, although I will not guide you through the Anaconda installation. Instead you can follow e.g. https://github.com/ageron/handson-ml3/blob/main/INSTALL.md. On Windows you may have to change a few system PATH settings, if the libraries are not detected by Visual Code, or if you have different versions of Python.

Kaggle competitions

One way to practice machine learning is to participate in Kaggle competitions. We will demonstrate this with a competition for beginners: House Prices - Advanced Regression Techniques. There you can download the required data, which in this case is a rather small zip file.

How to read this guide

The source codes labeled as Jupyter Cell can be pasted in one python file in order to create a new Jupyter cell each time. The code labeled as Test is rather meant to deepen the understanding of the main code, but it is not required for any subsequent cell. There is also some code labeled as Output, which just shows you the result of one of those cells.

Machine learning with python

We start by importing the libraries numpy, pandas and matplotlib (usually abbreviated as np, pd and plt) that will help us to explore the data.

#%%

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Algorithm 2: Jupyter Cell

They provide three types of extensively used data containers.

Numpy Arrays

or ndarray typed variables are often used for numerical computations due to their better performance speed. The data is stored in n-dimensional arrays. E.g. a 1D array has the shape of a vector, a 2D array the shape of a matrix, etc. The type of data stored in any given ndarray must always be the same, but other than that the data can have any valid type.

Pandas DataFrames

are always 2 dimensional arrays, but in addition their rows and columns have a label as well. In this sense they are very similar to spreadsheets or SQL tables. Usually column lables describe the features of the data, while the row labels describe the name of each sample or instance. For this purpose dataframes can store data with different types, even when they are stored in the same dataframe variable.

Pandas Series

are the 1 dimensional version of dataframes. This means their row has a label, and they can contain mixed data types as well. Whenever we extract a single column from a dataframe, we can obtain a pandas series.

For beginners it can be helpful to print the type of these containers, because sometimes it can be hard to distinguish them.

Next we need to read the required data before analyzing it. There are multiple ways how this can be done by letting Python automatically download and extract the data, or even use SQL directly in Jupyter cells in order to handle large datasets efficiently.

However, we want to keep it simple for now. This means you can download and extract the train.csv and test.csv files manually from the Kaggle competition, and save them in a folder of your choice. In the source code below you need to insert the name of this folder in the variable sLocal_Folder_Path.

#%%

from pathlib import Path
from IPython.display import display
sLocal_Folder_Path = "C:/Users/.../" #add your own folder name
housing = pd.read_csv(Path( sLocal_Folder_Path + "train.csv" ))
housing_test = pd.read_csv(Path( sLocal_Folder_Path + "test.csv" ))
display(housing)
display(housing_test)

Algorithm 3: Jupyter Cell

Here we have stored the data as housing and housing_test dataframe variables.

After running this cell you will see the table structure of housing and housing_test. Notice that we imported and used the display function in order to create two display outputs in the interactive window from only one cell. The output should show you a few example rows from each dataframe.

It should also tell you that housing has 81 columns, while housing_test has only 80 columns. The missing column are the housing sales prices that we will have to predict before submitting it on Kaggle. This means the data from housing will be used to train our prediction models.

One way to get a grasp on large datasets is to plot the histogram of all numerical features. The numerical values are grouped together in bins that are arranged along the x-axis. The bar length along the y-axis shows how many samples occured in each bin. The following code plots the histograms for each feature next to each other.

# %%

housing.hist(bins=50, figsize=(30,25))
plt.show()

Algorithm 4: Jupyter Cell

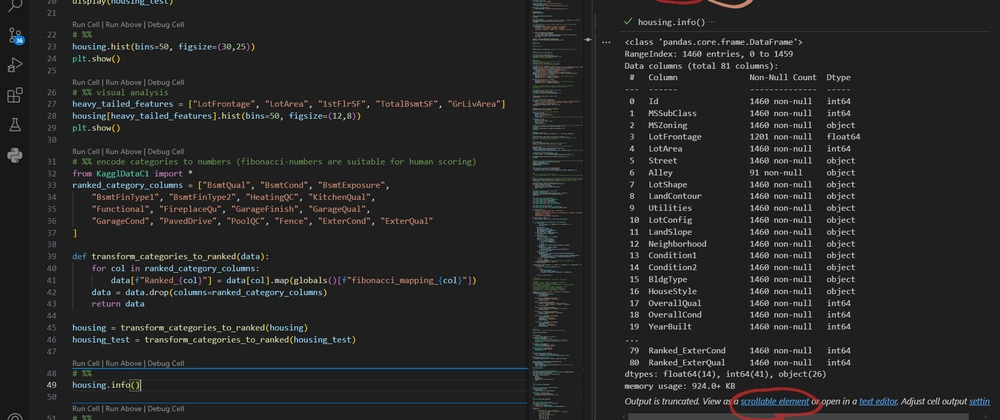
One important property to look for in these histograms are so called heavy-tailed distributions like the one on the left of the figure below.

Figure 1: Heavy-tailed features in the housing dataset (generated by deepseek)

They can be usually converted to bell-shaped normal distribution by calculating the logarithmus of the numerical values along the x-axis. Normal distributions are handles much better by machine learning tools than heavy tailed distributions. For now we will not worry about transforming the data. Instead, we simply look for heavy-tailed features in the housing data, and list them in heavy_tailed_features in order to use it later.

# %%

heavy_tailed_features = ["LotFrontage", "LotArea", "1stFlrSF", "TotalBsmtSF", "GrLivArea"]
housing[heavy_tailed_features].hist(bins=50, figsize=(12,8))
plt.show()

Algorithm 5: Jupyter Cell

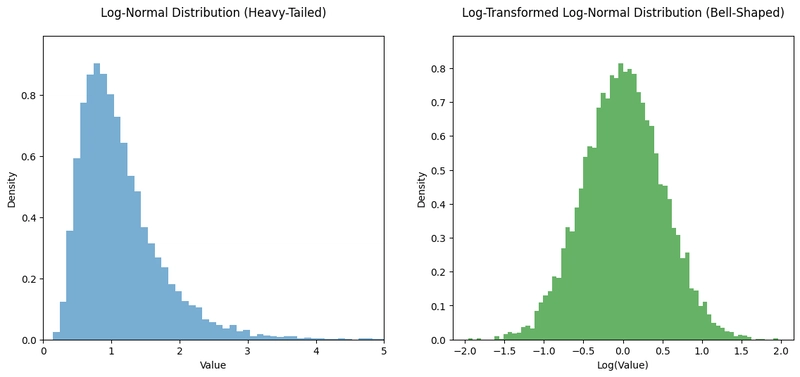
The output of the cell above shows the heavy-tailed features only as demonstrated in the following figure.

Figure 2: Heavy-tailed vs. normal distribution

Of course there are non-numerical features in the housing dataset as well. Fortunately, there is a file data_description.txt from the zip-file we downloaded earlier on Kaggle. If you open it in a text-editor, you can see a description of all features like e.g.

# %%

ExterQual: Evaluates the quality of the material on the exterior
     Ex  Excellent
     Gd  Good
     TA  Average/Typical
     Fa  Fair
     Po  Poor

Algorithm 6: Snippet from data_description.txt

Thanks to this description we can try to convert the feature ExterQual into a numerical one. It may seem curious at first, but since evaluations like Excellent or Poor are based on human estimations, it makes sense to use fibonnaci-numbers rather than linearly increasing numbers in order to map this kind of features to integer numbers. The reason behind this is that the difference between two adjacent numbers in a fibonnaci sequence is increasing based on the previous number in the sequence. Otherwise humans would have a harder time to distinguish between them (for more details see e.g. Scrum).

You may still be sceptical whether it makes sense to use fibonnaci-numbers for all non-numerical features, but for the sake of this guide we want to see a simple technique to produce numerical values. In addition, we will see that the numerical value of ExterQual is pretty good for predicting house sales prices.

Of course there are also features, where it does not make much sense to convert them to any number like for e.g. the roof material in the house data. They will stay untouched for now.

For our feature-to-number-mapping we can use dictionaries in Python. Since putting all feature-mapping dictionaries in one .py file would clutter the code, we store them in a file KagglDataC1.py instead, and put this file in the same folder as our main Python script.

# %%

# ExterQual: Evaluates the quality of the material on the exterior
fibonacci_mapping_ExterQual = {
    "Po" : 1,    # Poor
    "Fa" : 2,   # Fair
    "TA" : 3,   # Average/Typical
    "Gd" : 5,  # Good
    "Ex" : 8,  # Excellent
}

Algorithm 7: Snippet from KagglDataC1.py

The complete file can be found on my Github page (see KagglData.py), but you can also create it yourself with the methods I showed you.

Now we can go back to our main Python file, and add the following cell.

# %%

from KagglDataC1 import *
ranked_category_columns = ["BsmtQual", "BsmtCond", "BsmtExposure", 
    "BsmtFinType1", "BsmtFinType2", "HeatingQC", "KitchenQual", 
    "Functional", "FireplaceQu", "GarageFinish", "GarageQual",
    "GarageCond", "PavedDrive", "PoolQC", "Fence", "ExterCond", "ExterQual"]
def transform_categories_to_ranked(data):
    for col in ranked_category_columns:
        data[f"Ranked_{col}"] = data[col].map(globals()[f"fibonacci_mapping_{col}"])
    data = data.drop(columns=ranked_category_columns)
    return data
housing = transform_categories_to_ranked(housing)
housing_test = transform_categories_to_ranked(housing_test)

Algorithm 8: Jupyter Cell

This imports the contents of the KagglDataC1.py file, automatically converts features like ExterQual to a numerical value, adds them as new features in the dataframes housing and housing_test, and deletes the columns of the original non-numerical features. Here we chose to add the prefix Ranked_ to the new features in order to distinguish from the old ones.

Of course we should check, whether the modified housing dataframes are correct. One way to do that is to run

# %%

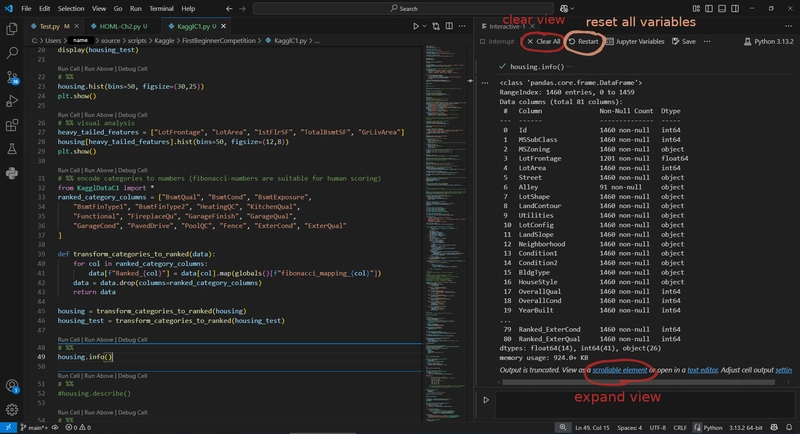
display(housing_test.info())
display(housing.info())

Algorithm 9: Jupyter Cell

which uses the .info() method for showing a list of all features (i.e. columns) of our housing dataframes together with their data type and the amount of instances for each feature.

E.g. int64 stands for integers, float64 for float values, whereas object indicates a non-numerical feature type.

If an output like the one from .info() is too large, you can still display the whole output by clicking on scrollable element in Visual Code. If everything went fine, then it should look like this.

Figure 3: Visual Code showing housing info

If there is no option to show the complete output, then it is probably because there are too many columns/features in your dataset. Fortunately you can fix this by changing the settings with a code like

# %%

pd.set_option('display.max_info_columns', 250)
pd.set_option('display.max_rows', 250)

Algorithm 10: Jupyter Cell

For the output of .info() the setting max_info_columns is enough, but we also want to set max_rows for other outputs as well (e.g. when we display the correlation matrix later on).

Another way of looking at the housing dataset is to run

# %%

housing.describe()

Algorithm 11: Jupyter Cell

which will show you information like the mean-value or the minimum/maximum values of all numerical features in the housing dataframe.

The set of numerical features can be further divided in continuous and discrete ones. The discrete features are the ones, where there is only a limited and rather small set of possible values for all samples of this feature. E.g. the housing feature OverallQual has only integer values from 1 to 10. We can see this by running the following code

# %%

(housing["OverallQual"]).value_counts().sort_index()

Test

which results in the output

OverallQual

1      2
2      3
3     20
4    116
5    397
6    374
7    319
8    168
9     43
10    18
Name: count, dtype: int64

Output

As you can see there are only 2 hourses with a terrible OverallQual of 1. Now is a good time to use these methods to explore some of the other features on your own before moving on. Maybe you can find some interesting observations. E.g. you may want to look at how many kitchen or other types of rooms the house samples have.

Later on we will modify the housing dataset for temporary purposes (e.g. stratified samples). This is why we want to make a copy of its current version, so we can undo the changes. Note that copying the dataframe is not the same as using a simple dataframe variable assignment, which would simply pass it per reference instead of passing it per value.

# %%

housing_original = housing.copy()

Algorithm 12: Jupyter Cell

Before we modify housing, we should look at the so called standard correlation coefficients between each feature. Without going into too much details, the correlation measures the linear dependency between two features. If a more complex dependency exists, or if there is no dependency at all, then the correlation should be close to 0. Otherwise it will be either close to +1 or to -1. Of course it can be possbile to transform non-linear dependencies into linear ones before measuring the correlations, but we will not dive too deep into this topic.

For now it is enough to know that these correlations can be easily obtained from the correlation matrix. Since we are very much interested in the correlation of the sale price and every other feature, we only have to look up the SalePrice column of the correlation matrix as demonstrated in the code below.

# %%

corr_matrix = housing.corr(numeric_only = True)
corr_matrix["SalePrice"].sort_values(ascending = False)

Algorithm 13: Jupyter Cell

If you run this cell, you should get a list of the correlations of each future (with respect to the house sale price). It should not surprise you too much that SalePrice has a correlation of 1.0 with itself.

More interesting examples are OverallQual, which has a high correlation of 0.79. There are also features we derived from the fibonnaci-numbers with a relatively high correlation (e.g. Ranked_ExterQual has 0.69 and Ranked_KitchenQual has 0.68).

If the absolute value of the correlations is high, then it is a good indicator that we have found an important feature. The advantage of this method is that is quite easy to find those features.

Of course it may be also possible that we miss some of the other important features, if their correlation is close to 0. In those cases we would need to use more sophisticated analysis methods.

Creating new features

Our next goal is to create completely new features based on some of the old ones in order to gain more meaningful information for predicting house sale prices. This means we have to make some educated guesses that are tailored more specifically to the concrete problem (in this case predicting house prices) instead of using very general methods like our previous fibonnaci-mapping. Here are some thoughts:

• There are features in the housing dataset, which count the amount of full bathrooms FullBath (including a shower) and HalfBath (i.e. toilets only) separately. Furthermore, these numbers do not take into account the baths in the basement (BsmtFullBath and BsmtHalfBath). By computing the sum of these four features, we get a more meaningful number of the total amount of bathrooms.
• The total area GrLivArea of living space (basement not included) is already an important feature, but if we multiply it with OverallQual we may get an even more meaningful feature.
• The fibonnaci-ranked features Ranked_PavedDrive, GarageFinish, Ranked_GarageQual, GarageCars and GarageArea probably have a positive impact on each other. Therefore, it can make sense to compute their product.
• The same is probably true for the quality of the heating Ranked_HeatingQC and the total amount of rooms TotRmsAbvGrd (basement not included).
• Ratios like the amount of bedrooms per living area, or the amount of toilets per bedroom can also lead to important new features.

We can translate these ideas in the code below. Note that when we compute the ratios, we have to be careful not to divide by 0. In our example we solve this problem by checking whether the feature of a given sample is 0, and then provide an alternative feature that is guaranteed to have a different value than 0.

# %%

housing["bath_sum"] = \
    housing["FullBath"] + housing["HalfBath"] \
    + housing["BsmtFullBath"] + housing["BsmtHalfBath"]
housing["areaquality_product"] = housing["GrLivArea"] * housing["OverallQual"]
housing["garage_product"] = housing["Ranked_PavedDrive"] \
    * housing["Ranked_GarageFinish"] * housing["Ranked_GarageQual"] \
    * housing["GarageCars"] * housing["GarageArea"]
housing["bedrooms_ratio"] = housing["BedroomAbvGr"] / housing["GrLivArea"]
housing["roomquality_product"] = housing["Ranked_HeatingQC"] \
    * housing["TotRmsAbvGrd"]
housing["bath_kitchen_ratio"] = np.where(
    housing["KitchenAbvGr"] != 0,  # Condition
    (housing["bath_sum"]) / housing["KitchenAbvGr"],  # True: Perform division
    (housing["bath_sum"]) / housing["TotRmsAbvGrd"]
)
housing["bath_bedroom_ratio"] = np.where(
    housing["BedroomAbvGr"] != 0,  # Condition
    (housing["bath_sum"]) / housing["BedroomAbvGr"],  # True: Perform division
    (housing["bath_sum"]) / housing["TotRmsAbvGrd"]
)

Algorithm 14: Jupyter Cell

Afterwards we can quickly check how the correlations of the new features look like compared to the old ones.

# %%

corr_matrix = housing.corr(numeric_only = True)
corr_matrix["SalePrice"].sort_values(ascending = False)

Algorithm 15: Jupyter Cell

The new output tells us e.g. that areaquality_product has the highest correlation of any other feature, which is already an improvement. We can also see that garage_product has a significantly higher correlation than any of its factors.

We could go further by dropping the old features after replacing them with better ones, or use advanced techniques like the principal component analysis (PCA), but for the sake of keeping this guide simple we will leave the old and new features as they are right now.

If we do not want to rely too much on the correlation coefficients, we can also use the so called scatter matrix, where each feature is plotted against each other. This can help to find out non-linear dependencies or clusters. Of course we can also find non-existing dependencies, if the plotted points are mostly aligned around a vertical or horizontal line the plot.

Note that plotting a feature against itself does not result in any interesting plot, which is why they are replaced by their corresponding histogram.

# %%

from pandas.plotting import scatter_matrix
attributes = ["SalePrice", "garage_product", "areaquality_product", 
    "roomquality_product", "bedrooms_ratio"]
scatter_matrix(housing[attributes], figsize=(10, 10))
plt.show()

Algorithm 16: Jupyter Cell

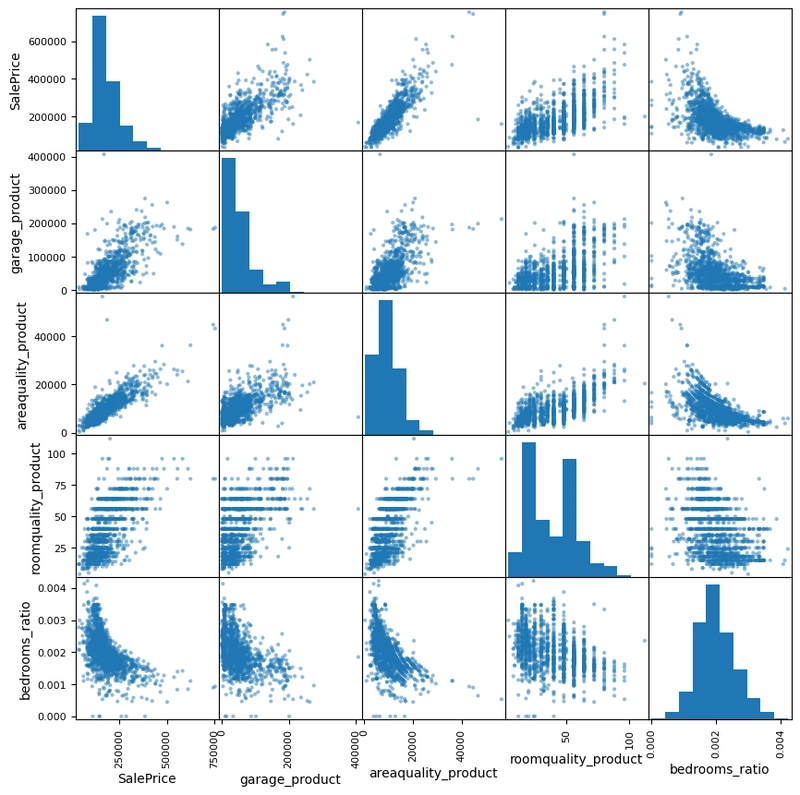
As a result we obtain the following plot. It shows e.g. how our bedrooms ratio has a non-linear dependency with other features like the sale price.

Figure 4: Scatter matrix

Strata

Before we can apply prediction models on our data, we have to test its performance. Of course we cannot test the performance very easily on the dataset of housing_test, because it is missing the sale prices. Therefore, we can only use housing for training and testing the quaility of our predictions.

For this purpose it is important to split the housing data into a training and a test set. Otherwise we would test its performance on the same set, where our prediction model has been trained. This can lead to a false overconfidence for our prediction model, which is probably going to fail on unknown data.

E.g. one common problem is overfitting, where a prediction model attempts to fit so many parameters that it can predict the outcome of the training set very well or even without any errors, but when it is applied to a different dataset it suddenly performs very poorly.

So now we have to find a good way to split the housing data. One possible way is use a random split, where hashing functions can help to consistently split the data, even if new data is added to the training set some time in the future.

However, in our case we do not want a random split in order to avoid that certain categories in important features are not under- or overrepresented in the training vs. the testing data. E.g. if we want to predict the performance of a new drug, then we want to represent the ages of all patients as evenly as possible. Of course we would have to group different ages together, i.e. we could divide the ages into different bins for the ages 0-10, 10-20, 30-40, etc.

This method is called stratified sampling. In our case we have to make an educated guess to find good strata for predicting house prices. E.g. we could use the areaquality and the bedrooms_ratio as stratas. For this purpose we use the function pd.cut, where the bins define each strata group and label them with the function argument labels.

# %%

strata_cat_1 = pd.cut(
    housing["areaquality_product"],
    bins = [0, 5e3, 8e3, 12e3, np.inf],
    labels = [1,2,3,4],
    include_lowest = True
)
strata_cat_2 = pd.cut(
    housing["bedrooms_ratio"],
    bins = [0.0, 16e-4, 21e-4, np.inf],
    labels = [1,2,3],
    include_lowest = True
)
strata_cat_1.value_counts().sort_index().plot.bar(grid = True)
plt.show()
strata_cat_2.value_counts().sort_index().plot.bar(grid = True)
plt.show()

Algorithm 17: Jupyter Cell

Also note that we used the argument include_lowest in order to prevent the case, where the edge cases are not included, i.e. if e.g. the bedrooms_ratio is 0 for a given sample. then pd.cut would convert it into NaN (not any number), because the bins start at 0, which is the outermost left edge.

The resulting plots show us the histograms for both strata features. Just to make sure that pd.cut did not create any NaN values, we can check this quickly with the following code.

# %%

has_nan = strata_cat_2.isna().any().any()  # Returns True if any NaN exists
print("Does the DataFrame contain NaN values?", has_nan)

Test

One problem we have not addressed, yet, is that we can split the housing dataset only with respect to one feature. If we wanted to combine two features, then we would have to use the following trick.

# %%

sStrataCat = "Strata_Cat"
housing[sStrataCat] = strata_cat_1.astype(str) + "_" + strata_cat_2.astype(str)
housing[sStrataCat].value_counts().sort_index().plot.bar(grid = True)

Algorithm 18: Jupyter Cell

Here we simply concatenate the strings of the labels of each strata feature, and use the resulting string as labels for the combined stata feature. The only problem is that some of the combined strata have very view samples, which could lead to a distortion of the prediction models or even to runtime errors.

In order to avoid this, we can put all underrepresented strata into a new stratum called Other, which covers the miscellaneous cases. Here the integer iMinCounts defines the minimum amount of samples each strata needs to have without being merged with the Other stratum.

# %%

iMinCounts = 100
housing_stratacat_counts = housing[sStrataCat].value_counts()
indices_of_small_housing_stratacat_counts = housing_stratacat_counts[
    housing_stratacat_counts < iMinCounts
].index
housing[sStrataCat] = housing[sStrataCat].apply(
    lambda x: 'Other' if x in indices_of_small_housing_stratacat_counts else x
)
housing[sStrataCat].value_counts().sort_index().plot.bar(grid = True)
plt.show()

Algorithm 19: Jupyter Cell

The resulting histogram looks much better now, after the small strata have vanished.

Now we that we have obtained the desired strata, we can revert the housing dataset back to the previous ones. In order split the data into a training and test set with respect to the strata we can use the library function train_test_split.

# %%

from sklearn.model_selection import train_test_split
housing_strata_category = housing[sStrataCat].copy()
housing = housing_original
strat_train_set, strat_test_set = train_test_split(
    housing, test_size = 0.15, stratify = housing_strata_category, random_state = 42
)
housing = strat_train_set.drop("SalePrice", axis=1)
housing_labels = strat_train_set["SalePrice"].copy()

Algorithm 20: Jupyter Cell

Pipelines

Before we can apply prediction models, we still have to make an important step. Pipelines are very helpful to transform the original dataset in a chain of several transformations. Even though we have already seen how transformations can be done manually (when we created new features), pipelines give us more control over the dataset.

E.g. pipelines allow us to try different variations of these transformations, and to even automate this process. Before we get to this point, we need to import the required library classes and functions from sklearn.

# %%

from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.compose import ColumnTransformer
from sklearn.compose import make_column_selector
from sklearn.preprocessing import FunctionTransformer
from sklearn.pipeline import Pipeline
from sklearn.base import BaseEstimator, TransformerMixin

Algorithm 21: Jupyter Cell

Then we define the features for the housing data that will be used to creat the new featurs.

# %%

list_trafo_columns = [
    "FullBath", "HalfBath", "BsmtFullBath", "BsmtHalfBath",
    "GrLivArea", "OverallQual",
    "Ranked_PavedDrive", "Ranked_GarageFinish", "Ranked_GarageQual", "GarageCars", "GarageArea",
    "BedroomAbvGr", "GrLivArea",
    "Ranked_HeatingQC", "GrLivArea",
    "KitchenAbvGr", "BedroomAbvGr", "TotRmsAbvGrd",
]

inverse_list_trafo_columns = {
    value: index for index, value in enumerate(list_trafo_columns)
}

Algorithm 22: Jupyter Cell

These features are all listed in list_trafo_columns. We will see in a moment, why we also need the inversion of this list, i.e. the dictionary inverse_list_trafo_columns.

Next we need to define a class that can transform the dataset features, i.e. we need a column transformer. This transformer is initialized by the __init__ function as demonstrated in the code below. Here __init__ allows us to use arguments like sum which can contain the column names of the features that will be added together (like e.g. when adding the amount of baths, half baths, etc.). Similarly, we can define the features for the products, for the denominator (in case we need a fraction for ratios), and an alternative denominator (in case one sample the orignal denominator column is 0).

Furthermore, we want to allow some variations to the column transformation. In order to keep the example a bit simpler, we only allow variations for the way the sum is computed with respect to some weights (sumweights). E.g. it may be possible that half baths get a smaller weight than full baths, or that basement baths have a smaller weight than baths above the ground.

# %%

class ColumnFormulaTransformer(BaseEstimator, TransformerMixin):
    def __init__(self,
            sum = [], product = [], denominator = [], altdenominator = [],
            sumweights = []
        ):
        self.sum = sum
        self.product = product
        self.denominator = denominator
        self.altdenominator = altdenominator
        self.sumweights = sumweights
    def fit(self, X, y=None, sample_weight=None):
        self.n_features_in_ = X.shape[1]
        return self
    def transform(self, X):
        assert self.n_features_in_ == X.shape[1]
        #calculate nominator:
        numerator = np.zeros(X.shape[0])
        for id, col in enumerate(self.sum):
            if id < len(self.sumweights):
                weight = self.sumweights[id]
            else:
                weight = 1
            numerator += X[:,inverse_list_trafo_columns[col]] * weight
        if self.product:
            prodnumerator = np.ones(X.shape[0])
            for col in self.product:
                prodnumerator *= X[:,inverse_list_trafo_columns[col]]
            numerator += prodnumerator
        #calculate denominator:
        if self.denominator:
            denominator = X[:, inverse_list_trafo_columns[self.denominator[0]]]
            if self.altdenominator:
                altdenominator = \
                    X[:, inverse_list_trafo_columns[self.altdenominator[0]]]
                denominator[denominator == 0] = altdenominator[denominator == 0]
            result = numerator / denominator
        else:
            result = numerator
        return result.reshape(-1, 1) #convert result from 1D to 2D NumPy array
    def get_feature_names_out(self, names=None):
        return ["formula"]

Algorithm 23: Jupyter Cell

This may be a bit overwhelming, but will help to understand the versatiliy of the column transformer method. Another important part of transforming the data is making sure that sample with missing features are handled correctly. One solution is to replace the missing values with a median value (works for numerical features only), or to replace them by the most frequent one (which also works for categorical features).

Replacing missing features is handled relatively simply with the SimpleImputer.

# %%

def make_pipeline_with_formula(
        sum = [], product = [],
        denominator = [], altdenominator = []
    ):
    return Pipeline([
        ("imputer", SimpleImputer(strategy="median")),
        (
            "ratio",
            ColumnFormulaTransformer(
                sum = sum, product = product,
                denominator = denominator, altdenominator = altdenominator
            )
        ),
        ("scaler", StandardScaler())
    ])

Algorithm 24: Jupyter Cell

At the botton of this pipeline you can also see the StandardScaler, which is another transformer that center the sample values around the mean value and normalizes the variance. You do not have to understand the details here, but you should know that machine learning algorithms can perform better, if the numerical values are transformed by the standard scaler. Of course we need to apply the standard scaler as the last step in order make use of this advantage.

Before we insert the arguments for the column transformer, it is much more convenient to arrange them in ColumnTransformer_TupleList. You will see why in a moment.

# %%

bathsum_list = ["FullBath", "HalfBath", "BsmtFullBath", "BsmtHalfBath"]
ColumnTransformer_TupleList = [
    ("bath", make_pipeline_with_formula(
            sum = bathsum_list
        ), list_trafo_columns
    ),
    ("areaquality", make_pipeline_with_formula(
            product = ["GrLivArea", "OverallQual"]
        ), list_trafo_columns
    ),
    ("garage", make_pipeline_with_formula(
            product = ["Ranked_PavedDrive", "Ranked_GarageFinish",
                    "Ranked_GarageQual", "GarageCars", "GarageArea"]
        ), list_trafo_columns
    ),
    ("bedroom", make_pipeline_with_formula(
            product = ["BedroomAbvGr"], denominator = ["GrLivArea"]
        ), list_trafo_columns
    ),
    ("roomquality", make_pipeline_with_formula(
            product = ["Ranked_HeatingQC", "TotRmsAbvGrd"]
        ), list_trafo_columns
    ),
    ("bath_kitchen", make_pipeline_with_formula(
            sum = bathsum_list,
            denominator = ["KitchenAbvGr"],
            altdenominator = ["TotRmsAbvGrd"]
        ), list_trafo_columns
    ),
    ("bath_bedroom", make_pipeline_with_formula(
            sum = bathsum_list,
            denominator = ["BedroomAbvGr"],
            altdenominator = ["TotRmsAbvGrd"]
        ), list_trafo_columns
    ),
]

Algorithm 25: Jupyter Cell

We also have to set up the simple pipelines. E.g. one of them manages the logarithmus-transformations of the heavy-tailed features. Then we can add them to our ColumnTransformer_TupleList.

# %%

def safe_log(x):
    return np.log(np.where(x <= 0, 1e-10, x))

log_pipeline = make_pipeline(
    SimpleImputer(strategy = "median"),
    #FunctionTransformer(np.log, feature_names_out = "one-to-one"),
    FunctionTransformer(safe_log, feature_names_out = "one-to-one"),
    StandardScaler()
)

cat_pipeline = make_pipeline(
    SimpleImputer(strategy="most_frequent"),
    OneHotEncoder(handle_unknown="ignore")
)

default_num_pipeline = make_pipeline(
    SimpleImputer(strategy = "median"),
    StandardScaler()
)

ColumnTransformer_TupleList.extend([
    ("log", log_pipeline, heavy_tailed_features),
    ("cat", cat_pipeline, make_column_selector(dtype_include = object)),
])

Algorithm 26: Jupyter Cell

You may wonder what OneHotEncoder is good for. It takes categorical (i.e. non-numerical) features and assigns each category to a new feature, where they can have only 0 or 1 as a numerical value. In this way the categories are not mixed up. Otherwise the prediction models could assume that there was a numerical order between two different categories, even though that would not make any sense. Therefore, each category can have only 1 as a value in one of the features and 0 in any other feature, which gives the one hot encode its name.

Prediction models

Now we can finally use prediction models in combination with out pipeline. For now you do not need to know how these models work. There are many different models, but the way they are handled in the Python code is quite similar. For our purposes the so called RandomForestRegressor is quite good.

However, prediction models cannot optimize all variables by themselves. These variables are called hyperparameters. For e.g. the sum weights we discussed earlier can be seen as hyperparameters. We do not need to set them ourselves. Instead this is managed by RandomizedSearchCV.

# %%

from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniform, randint

full_pipeline = Pipeline([
    ("preprocessing", preprocessing),
    ("random_forest", RandomForestRegressor(random_state=42)),
])

class CustomSumweightsSampler:
    def rvs(self, random_state=None):
        #["FullBath", "HalfBath", "BsmtFullBath", "BsmtHalfBath"]
        return [1.0, uniform(0.0, 1.0).rvs(random_state=random_state),
                uniform(0.0, 1.0).rvs(random_state=random_state),
                uniform(0.0, 1.0).rvs(random_state=random_state)]

param_distribs = {
    'preprocessing__bath_kitchen__ratio__sumweights': CustomSumweightsSampler(),
    'preprocessing__bath_bedroom__ratio__sumweights': CustomSumweightsSampler(),
    'preprocessing__bath__ratio__sumweights': CustomSumweightsSampler(),
}

Algorithm 27: Jupyter Cell

The way it works, that the hyperparameters are randomly generated until the best set of variations is found. In order to evaluate each variation, the RandomizedSearchCV splits the dataset with respect to the labels (in this case the house price sales).

This should not be confused with the strata we discussed earlier, because when the model performance is evaluated, only the labels really matter for the strata. The method used here is called cross validation. It subdivides the training sets in $k$ many subsets, removes one of them, uses the remaining $k-1$ subsets to train the model and uses the previously removed subset to evaluate the performance of the prediction model. The amount of subdivision is controlled by the function argument cv for RandomizedSearchCV as demonstrated below.

# %%

rnd_search = RandomizedSearchCV(
    full_pipeline,
    param_distributions = param_distribs,
    n_iter=15,
    cv=10,
    scoring='neg_root_mean_squared_error',
    random_state=42
)
rnd_search.fit(housing, housing_labels)

Algorithm 28: Jupyter Cell

Then one can see the test results for the resulting errors of the prediction model with respect to the cross validation.

# %%

cv_rmse_scores = -rnd_search.cv_results_['mean_test_score']
rmse_summary = pd.Series(cv_rmse_scores).describe()
rmse_summary

Algorithm 29: Jupyter Cell

Finally, we can use the prediction model to predict the labels (i.e. the sale prices) of the dataset, where the labels are unknown.

# %%

housing_predicted_prices = rnd_search.predict(housing_test)
submission = pd.DataFrame({
    'Id': housing_test['Id'],
    'SalePrice': housing_predicted_prices
})
submission.to_csv(sLocal_Folder_Path + '/submission.csv', index=False)

Algorithm 30: Jupyter Cell

In this case the predicted values are saved as a file called submission.csv. This file can then be uploaded on Kaggle, where you can see your test results in form of the root mean squared error.

If this error is below 0.20, you have decent result for this competition. Below 0.15 is a solid result, and below 0.10 means you are really good. In our case we reach a score of about 0.14.

References

• Aurélien Géron (2019). Hands-On Machine Learning with Scikit-Learn, Keras, and Tensorflow: Concepts, Tools, and Techniques to Build Intelligent Systems. O'Reilly Media
• Jeff Sutherland (2014). Scrum: The Art of Doing Twice the Work in Half the Time. Crown Currency