Problem description
Given a non-empty array of integers, every element appears twice except for one. Find that single one.
Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
Example 1:
Input: [2,2,1]
Output 1
Example 2:
Input: [4,1,2,1,2]
Output: 4
Let's solve
As I mentioned in the introductory post, if you're a beginner don't solve while trying to achieve the optimal runtime complexity in your first try. So, ignore the Note.
Approach 1
If you're not familiar with a fancy data structure like Hash Map(aka Dictionary) you would have thought that if an element doesn't exist to the left and to the right in the array then it is the single number and you're right!.
Algorithm:
- Iterate over all elements of the array
- Let the current element be ele and index be idx
- If ele doesn't exist in array[:idx] and array[idx+1:] then return ele
Code:
def approach1(nums):
for idx in range(len(nums)):
ele = nums[idx]
if ele not in nums[:idx] and ele not in nums[idx+1:]:
return ele
Complexity analysis:
Time complexity: O(n^2)
Space complexity: O(1)
Approach 2
Upon careful analysis of the previous code, the main bottleneck is that we don't know where the 2nd occurrence of an element resides. Hence, we are forced to search for every element to the left and right of the current element.
What if we did something to the array so that we knew where the 2nd occurrence is for each element?
Sorting to the rescue!
Sorting a list of numbers means arranging them in an increasing or decreasing order.
How does this help?
Since each element occurs twice except a single element, in the sorted array similar elements will be next to each other.
Example 1:
Input: [4, 1, 2, 1, 2]
Sorted Output: [1, 1, 2, 2, 4]
Example 2:
Input: [6, 2, 4, 1, 3, 4, 1, 2, 6]
Sorted Output: [1, 1, 2, 2, 3, 4, 4, 6, 6]
Now, we see that we can easily find the element that occurs once because if it is in the middle then it will be at an even indexed position otherwise it'll be at either end of the array.
Algorithm:
- Sort the array and let len = length of array
- If len == 1 then return array[0]
- If array[0] != array[1] then return array[0]
- If array[len - 1] != array[len - 2] then return array[len - 1]
- Iterate over even indexed elements and if array[i] != array[i + 1] then return array[i]
Code:
def approach2(nums):
nums = sorted(nums)
length = len(nums)
if length == 1:
return nums[0]
if nums[0] != nums[1]:
return nums[0]
if nums[length - 1] != nums[ length - 2]:
return nums[length - 1]
for i in range(0, length, 2):
if nums[i] != nums[i + 1]:
return nums[i]
Complexity analysis:
Time complexity: O(n*log(n))
Space complexity: O(1)
Approach 3
If we sort the array, then it will be slow for really huge arrays.
Let's take a step back and observe how a person with no programming knowledge whatsoever would solve this. Let's call this person Saitama.
Saitama would take a paper and write down each element and if its count is greater than 1, then he would either strike it or increment the count.
Then he would go through this list looking for the element that wasn't struck or whose count is equal to 1.
But how do we get this magical notebook where we can note down elements and their counts in code?
Introducing the Map ADT
A Map is an abstract data type(ADT) with the following properties:
- Consists of key-value pairs called items
- Each item must be unique and is identified by the key.
- You can add/modify/remove items only with the key
- Keys may also be modified
- It should be iterable by key or item
In short, it's like a dictionary where words and their meanings form an item. In a Map, a key is mapped to its value.
The most common implementation of the Map ADT is called Hash Map.
So, we can use a Hash Map to store the count of each element in the array.
Algorithm:
- Iterate over all elements of the array
- Update the count of the current element in hashmap
- Iterate over keys of hashmap
- If the value of the current key is 1 then return it
Code:
def approach3(nums):
hashmap = {}
for ele in nums:
hashmap[ele] = hashmap.get(ele, 0) + 1
for ele in hashmap:
if hashmap[ele] == 1:
return ele
Complexity analysis:
Time complexity: O(n + n*1) = O(2*n) = O(n)
Space complexity: O(n), the size of hashmap will grow with the size of nums
Now that we've learned about this new ADT let's try to use Map to solve this in one loop.
Remember how Saitama, struck off an element when it's count increased from 1? Let's do that! We just have to remove the item from the Map.
Code:
def approach3_improved(nums):
hashmap = {}
for ele in nums:
hashmap[ele] = hashmap.get(ele, 0) + 1
if hashmap[ele] > 1:
del hashmap[ele]
keys = list(hashmap.keys())
return keys[0]
Complexity analysis:
Time complexity: O(n)
Space complexity: O(n)
Approach 4
If you're decent at math then you may have observed that if the sum of the elements that occur twice is 'x' and the single number is 'y'
Sum of all elements = S1 = 2*x + y
But if we could somehow get the sum of all elements counted only once then
Sum of all unique elements = S2 = x + y
We need to find 'y', therefore
2*S2 - S1 = 2*(x + y) - (2*x + y)
2*S2 - S1 = 2*x + 2*y - 2*x - y
2*S2 - S1 = y
OR
y = 2*S2 - S1
Now that we've figured that out, all that is left to figure out a way to find the sum of unique elements in the array.
Enter Set
A Set is an abstract data type(ADT) with the following properties:
- Add/Remove a list of unique objects
- Test for existence of an object in the set
- It should be iterable
The most common implementation of the Set ADT is called Hash Set or Set.
So, we can use a set to store unique elements of the array to get S2.
Algorithm:
- Initialize empty set and variables setSum and normalSum to 0
- Iterate over all elements of the array
- If the element is not in the set then add to set and add value to setSum
- Add value to normalSum
- The required value is 2*setSum - normalSum
Code:
def approach4(nums):
hashset = set()
setSum = 0
normalSum = 0
for ele in nums:
if ele not in hashset:
hashset.add(ele)
setSum += ele
normalSum += ele
ans = 2*setSum - normalSum
return ans
Complexity analysis:
Time complexity: O(n)
Space complexity: O(n), the size of hashset will grow with the size of nums
Approach 5
If you're a beginner then be warned because this approach is not normal.
Watch this video to get an idea of how this solution compares to what you've done until now. Our solutions until now are like the Cyborg: Genos and this solution is like the Bald guy: Saitama.
So, what is the killer move in this solution? In competitive programming, we often use bitwise operators to solve certain problems efficiently. It can be to store, remove or identify data or patterns.
In this problem, we will use the famous bitwise XOR Operator.
You can read up on it in the link above, but I'll list out the important properties of this operator w.r.t numbers here:
In the above properties A, B and C are numbers and the circle with a cross inside is the symbol used to denote the XOR operator. In programming, it is usually performed with the '^' symbol.
Now, since A^A = 0, 0^0 = 0 and 0^A = A and order doesn't matter
If we XOR all the elements in the array the result will be the single number because the numbers that occur twice will result in 0 and when 0 is XORed with the single number the result is the same.
Here's an example to simplify things:
Input: [6, 2, 4, 1, 3, 4, 1, 2, 6]
Result = 6 ^ 2 ^ 4 ^ 1 ^ 3 ^ 4 ^ 1 ^ 2 ^ 6
Since order doesn't matter in XOR, we can rewrite it as
Result = 6 ^ 6 ^ 4 ^ 4 ^ 2 ^ 2 ^ 1 ^ 1 ^ 3
= ( 0 ) ^ ( 0 ) ^ ( 0 ) ^ ( 0 ) ^ 3
= 0 ^ 3
= 3
Now that it's clear we can do this in one loop, let's figure out how to solve it with no extra memory.
It's pretty simple, instead of storing the XORed result in a variable, we can use the elements of the array to store the XORed result until the corresponding index.
Algorithm:
- Iterate from index 1 in the array
- Assign array[i] = array[i] ^ array[i-1]
- return array[length - 1]
Code:
def approach5(nums):
for i in range(1, len(nums)):
nums[i] = nums[i] ^ nums[i-1]
return nums[-1]
Complexity analysis:
Time complexity: O(n)
Space complexity: O(0)
Summary
We've seen 5(6 overall) different approaches to solve this question.
Like I said the last approach is completely different but one pattern to note is that XOR helps in removing duplicate numbers as long as they come in even counts.
Here's a repl with a collection of all the above approaches. You can fork it and tweak it and try your own solutions.
I hope this post was useful, if you have any suggestions or doubts please comment below.



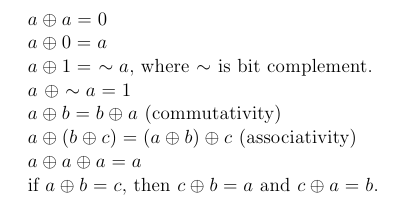


Top comments (0)