Floyd Warshall Algorithm is used to solve all pairs shortest path problem. We have to find shortest path from all nodes to all other nodes.
Graph that we will be using in this article is a directed weighted graph and we use it in adjacency matrix form in our program:
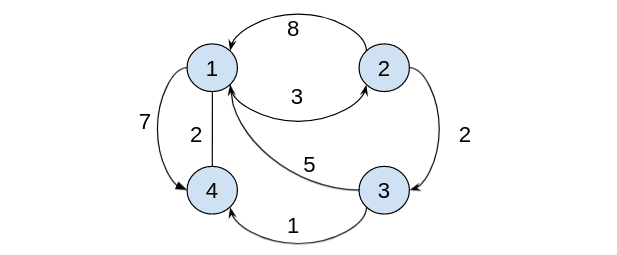
So how does Floyd Warshall algorithm works?
Floyd warshall algorithm is a dynamic programing method and hence makes a decision on every step which reduces our time complexity.
- First create a matrix with no nodes as intermediate node and let's call this array as being our A0. Each element in this represent distance from i to j where A0[i][j] is the element. Don't forget that arrays in Julia are 1-based, so A[1][1] is starting value in top left corner of the vector.
A^0 = [
[ 0, 3, Inf, 7],
[ 8, 0, 2, Inf],
[ 5, Inf, 0, 1],
[ 2, Inf, Inf, 0]
];
And its true that the initial matrix is same as our adjancency matrix.
- Now, subsequently create matrices A1, A2, A3, A4 which consider node 1, node 2, node 3, node 4 respectively as intermediate node and are built using previous matrice. For example, To create A1 we consider node 1 as our intermediate and update the distances if minimum distance value smaller than existing distance value found.
For like A1[2][3], new updated value will be
A1[2][3] = min(A0[2][3], A0[2][1] + A0[1][3])
Let see the change from A0 to A1:
A0:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, Inf, 7.0]
[8.0, 0.0, 2.0, Inf]
[5.0, Inf, 0.0, 1.0]
[2.0, Inf, Inf, 0.0]
A1:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, Inf, 7.0]
[8.0, 0.0, 2.0, 15.0]
[5.0, 8.0, 0.0, 1.0]
[2.0, 5.0, Inf, 0.0]
A1[1][1] = min(A0[1][1], A0[1][1] + A0[1][1]) = min(0,0) = 0
A1[1][2] = min(A0[1][2], A0[1][1] + A0[1][2]) = min(3,3) = 3
A1[1][3] = min(A0[1][3], A0[1][1] + A0[1][3]) = min(Inf,Inf) = Inf
A1[1][4] = min(A0[1][4], A0[1][1] + A0[1][4]) = min(7,7) = 7
A1[2][1] = min(A0[2][1], A0[2][1] + A0[1][1]) = min(8,8) = 8
A1[2][2] = min(A0[2][2], A0[2][1] + A0[1][2]) = min(0,0) = 0
A1[2][3] = min(A0[2][3], A0[2][1] + A0[1][3]) = min(2,2) = 2
A1[2][4] = min(A0[2][4], A0[2][1] + A0[1][4]) = min(Inf,8+7) = 15
A1[3][1] = min(A0[3][1], A0[3][1] + A0[1][1]) = min(5,5) =5
:
:
:
:
- Distances in the matrice Alast in which last is number of vertices and will be the one with the solution of all pairs shortest path problem and has minimum distances of a node to all other nodes.
Pseudo code:
let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
for each edge (u, v) do
dist[u][v] ← w(u, v) // The weight of the edge (u, v)
for each vertex v do
dist[v][v] ← 0
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if dist[i][j] > dist[i][k] + dist[k][j]
dist[i][j] ← dist[i][k] + dist[k][j]
end if
Code:
# All pairs shortest path
function FloydWarshall(dist)
println("Initial Adjacency matrix: ")
display(dist)
println("\n")
for k in 1:V
# pick all vertices as source one by one
println("Matrix A^k with k as ", k)
println("Current dist:")
display(dist)
println("\n")
for i in 1:V
# Pick all vertices as destination for the
# above picked source
for j in 1:V
# If vertex k is on the shortest path from
# i to j, then update the value of dist[i][j]
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
end
end
end
println("\nMatrix after applying Floyd Warshall: ")
display(dist)
println("\n")
end
graph = [[ 0, 3, Inf, 7],
[ 8, 0, 2, Inf],
[ 5, Inf, 0, 1],
[ 2, Inf, Inf, 0]
];
V = size(graph)[1] # Number of vertices in the graph
FloydWarshall(graph)
Output:
(base) ashwani@user:~/practice/DAY2$ julia floyd.jl
Initial Adjacency matrix:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, Inf, 7.0]
[8.0, 0.0, 2.0, Inf]
[5.0, Inf, 0.0, 1.0]
[2.0, Inf, Inf, 0.0]
Matrix A^k with k as 0
Current dist:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, Inf, 7.0]
[8.0, 0.0, 2.0, Inf]
[5.0, Inf, 0.0, 1.0]
[2.0, Inf, Inf, 0.0]
Matrix A^k with k as 1
Current dist:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, Inf, 7.0]
[8.0, 0.0, 2.0, 15.0]
[5.0, 8.0, 0.0, 1.0]
[2.0, 5.0, Inf, 0.0]
Matrix A^k with k as 2
Current dist:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, 5.0, 7.0]
[8.0, 0.0, 2.0, 15.0]
[5.0, 8.0, 0.0, 1.0]
[2.0, 5.0, 7.0, 0.0]
Matrix A^k with k as 3
Current dist:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, 5.0, 6.0]
[7.0, 0.0, 2.0, 3.0]
[5.0, 8.0, 0.0, 1.0]
[2.0, 5.0, 7.0, 0.0]
Matrix A^k with k as 4
Current dist:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, 5.0, 6.0]
[5.0, 0.0, 2.0, 3.0]
[3.0, 6.0, 0.0, 1.0]
[2.0, 5.0, 7.0, 0.0]
Matrix after applying Floyd Warshall:
4-element Vector{Vector{Float64}}:
[0.0, 3.0, 5.0, 6.0]
[5.0, 0.0, 2.0, 3.0]
[3.0, 6.0, 0.0, 1.0]
[2.0, 5.0, 7.0, 0.0]
Floyd Warshall Algorithm is usually faster than Dijsktra Algorithm which can also be used to solve this problem by take each node as source one by node and finding shortest paths to all other nodes.
Floyd Warshall Algorithm Complexity
Time Complexity
There are three loops. Each loop has constant complexities. So, the time complexity of the Floyd-Warshall algorithm is O(n3).
Space Complexity
The space complexity of the Floyd-Warshall algorithm is O(n2).
Floyd Warshall Algorithm Applications
- To find the shortest path is a directed graph
- To find the transitive closure of directed graphs
- To find the Inversion of real matrices
- For testing whether an undirected graph is bipartite






Top comments (0)