This article is being shared from the Codacy Code Quality Community, and was written by one of our members. Check out the original post here and feel free to join the community.
If you had an algorithm-related course as I did, you’ve probably heard of the term Big-O notation. It’s one of the most fundamental tools to analyze the cost of an algorithm before implementing it.
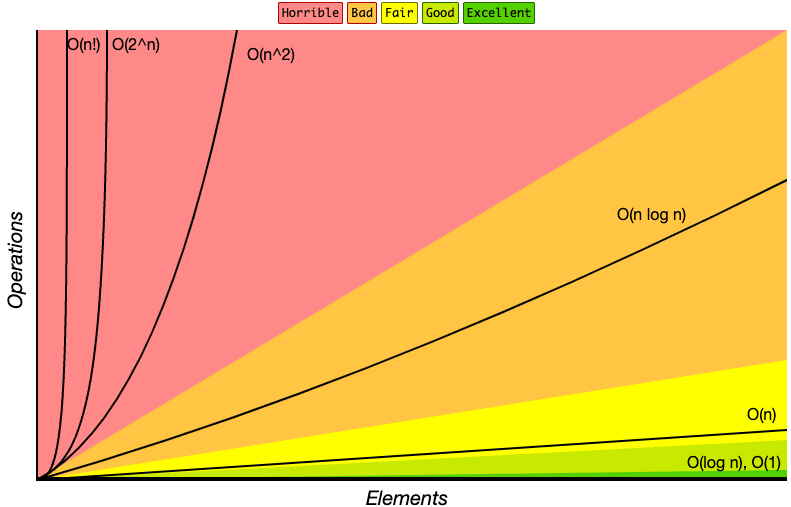
Big-O notation describes the complexity of your code using algebraic terms, but let’s take a simpler approach today when analyzing five typical Big-Os.
O(1) - constant complexity
No matter the input data set size, it will always take constant time (or space) to execute.
int constantExample(int x, int y) {
return x + y;
}
O(log(n)) - logarithmic complexity
Generally reduces the problem size with each iteration.
int logarithmicExample(int n) {
while (n > 1) {
n = n / 2;
}
}
O(n) - linear complexity
It increases linearly and in direct proportion to the size of the input.
boolean linearExample(IList elements, int value) {
foreach (var element in elements) {
if (element == value) return true;
}
return false;
}
O(n2) - quadratic complexity
It’s directly proportional to the square of the size of the input.
void quadraticExample(int array[], int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
print(array[i], array[j]);
}
}
}
O(2n) - exponential complexity
Its growth doubles with each addition to the input data set. A great example is the Fibonacci recursive function.
int fibonacci(int number) {
if (number <= 1) return number;
return fibonacci(number - 1) + fibonacci(number - 2);
}
💡 Do you want a Big-O cheatsheet? Head over here! You’ll find complexities for data structures and algorithms in the best, average, and worst-case scenarios.



Top comments (0)