DEV Community

CopyPasteEngineer
CopyPasteEngineer

Posted on

Python Coding ขำ ๆ: ลอง simulate สถานการณ์ COVID-19 แบบง่าย ๆ ด้วย Python part 1

#oop #python

สำหรับสถานการณ์ช่วงนี้ที่ทั้งโลกกำลังเผชิญหน้ากับ COVID-19 เจ้าหน้าที่ที่มีหน้าที่รับผิดชอบในเรื่องนี้คงต้องคิดกันจนปวดหัวนะครับ ว่าจะ take action หรือออก policy อย่างไร ภายใต้ทรัพยากรที่จำกัด เงินจำกัด และคนก็จำกัด ควรจะลงทุนกับการวิจัย vaccine ก่อนดี หรือจะแก้เฉพาะหน้าไปก่อนดี และแต่ละ action จะส่งผลอย่างไร มากหรือน้อย

ในการจะตอบคำถามต่าง ๆ นั้น ส่วนหนึ่งก็จำเป็นอาศัยการสร้าง model ทางคณิตศาสตร์ที่แม่นยำเพื่อทำนายผลในอนาคตล่วงหน้าเพื่อให้ทราบว่าสถานการณ์ข้างหน้ากำลังจะเป็นไปอย่างไร และถ้าทำอย่างนี้ไป จะเกิดอะไรขึ้น

ซึ่งงานในส่วนนี้โดยทั่วไปก็จะมี นักระบาดวิทยา (Epidemiologist) คอยทำหน้าที่ในการเก็บข้อมูลจริง เพื่อมาสร้างโมเดล หรือออกมาตรการรับมือต่าง ๆ อยู่แล้วครับ และยังมี model ทางคณิตศาตร์อื่น ๆ อีกมากที่สามารถใช้ในการทำนายได้จากหลากหลายสายงาน เช่น Data Scientist หรือ Economist ซึ่งสามารถให้ผลที่แม่นยำ และมี performance ในการคำนวณที่ดี เช่นกัน

SEIR-equation.png
ตัวอย่างโมเดลโรคระบาดในมุมของระบาดวิทยา: สมการ differential equation ของ SEIR Model (simplified)
(https://towardsdatascience.com/social-distancing-to-slow-the-coronavirus-768292f04296)

ในบทความนี้ เพื่อให้เข้าใจถึงความซับซ้อนของปัญหา และปัจจัยต่าง ๆ ที่ต้องคำนึงถึง จึงลองทำเป็น project simulation เล็ก ๆ ง่าย ๆ ขึ้นมาเล่น ๆ ให้มองว่าเป็น project ฝึกฝีมือเขียนโปรแกรมแบบ OOP ขำ ๆ โดยมีเป้าหมายเพื่อศึกษาดูการแพร่กระจายของ virus สมมุติชนิดหนึ่ง ชื่อว่า DIVOC-91 ซึ่งแพร่ระบาดบนโลกสมมุติแห่งหนึ่ง แล้วดูว่าถ้าเราเป็นรัฐบาลหรือเจ้าหน้าที่จะตัดสินใจออกมาตรการรับมืออย่างไร แบบง่าย ๆ ก่อน แล้วจากนั้นจะค่อย ๆ เพิ่มความซับซ้อนของ simulation ขึ้นเรื่อย ๆ ใน part ต่อ ๆ ไป เพื่อให้ใกล้เคียงกับโลกความเป็นจริงมากขึ้นครับ

Scenario

ใน part ที่ 1 นี้เพื่อความง่าย เราลองเริ่มจากสร้างโลกขึ้นมาแบบง่าย ๆ โดยการกำหนดเป็น rules ต่าง ๆ ออกมาดังนี้ครับ

  • โลกนี้มีประชากร 7,000 คน
  • คนแต่ละคนจะมี 3 สถานะ คือ สุขภาพดี, ติดเชื้อ, และ เสียชีวิต
  • ในแต่ละวัน คนที่ยังไม่เสียชีวิต (แน่นอน 555) แต่ละคนจะเดินทางไปพบเจอคนอื่นที่ยังไม่เสียชีวิต แบบสุ่ม 10 คน
  • ถ้าคนที่ ติดเชื้อ และคนที่ สุขภาพดี พบกัน คนที่สุขภาพดีจะมีโอกาสติดเชื้อ 10%
  • ในแต่ละวัน คนที่ ติดเชื้อ จะมีโอกาสเสียชีวิต 0.01% (ใจดีมาก)
  • แต่ถ้าไม่เสียชีวิต ในแต่ละวัน ผู้ติดเชื้อคนดังกล่าว จะมีโอกาสหาย กลับมาเป็น สุขภาพดี 1%
  • โดยจะเริ่มจากให้มีผู้ติดเชื้อ 1 คน ในวันแรกนะครับ

ใน part นี้ให้เงื่อนไขเป็นแบบง่าย ๆ ตามนี้ก่อน ซึ่งอาจจะดูไม่ค่อยสมจริงบ้าง ใน part ต่อ ๆ ไปก็จะค่อย ๆ เพิ่มเงื่อนไขเข้าไปนะครับ

Get Started

โค้ดของบทความนี้จะแชร์ไว้บน Google Colab ใน link นี้ นะครับ เพื่อความสะดวก สามารถแก้โค้ดและรันบน browser ได้ทันที ไม่ต้อง download หรือ install อะไรลงบนเครื่อง ผู้อ่านสามารถรันโค้ดจริงไปพร้อมกับอ่านบทความนี้ได้เลยครับ

วิธีการรันโค้ดใน colab notebook

  1. ให้คลิกที่ File มุมซ้ายบน แล้วเลือก Save a copy in drive... ก่อนนะครับ
  2. จากนั้นให้คลิกเลือก block ที่ต้องการจะรันแล้วกด Ctrl+Enter นะครับ

โดยในบทความจะหยิบเฉพาะโค้ดใน part ที่สำคัญ ๆ เช่น modelling บางส่วนมาอธิบายนะครับ และจะข้ามส่วนที่เป็นรายละเอียดเล็ก ๆ น้อย ๆ ไป เช่น function เสริมบางส่วน หรือการ plot graph แนะนำให้ลองดูโค้ดใน Colab ไปพร้อม ๆ กัน จะช่วยให้เข้าใจมากขึ้นครับ

เริ่มกันเลยนะครับ

ใส่ค่าคงตัวต่าง ๆ

จาก rules ต่าง ๆ ที่เรากำหนดขึ้นมา อย่างแรกผมเอาแค่คงตัวต่าง ๆ ใส่เข้าไปในโปรแกรมก่อนครับ ได้แก่

  • จำนวนประชากร (N_POPULATION)
  • จำนวนผู้ติดเชื้อเริ่มต้น (N_INFECTED_INIT)
  • จำนวนคนที่ไปพบเจอในแต่ละวัน (N_MEETINGS)
  • โอกาสติดเชื้อ (PROB_INFECT)
  • โอกาสเสียชีวิต (PROB_DIE)
  • โอกาสหาย (PROB_CURED)

โดยจะเก็บเป็น dict และส่งเป็น parameter เข้าไปให้กับตัว simulator นะครับ เพื่อให้สะดวก เวลาทดลองแก้ค่าต่าง ๆ

default_config = {
    'N_POPULATION': 7_000,
    'N_INFECTED_INIT': 1,

    'N_MEETINGS': 10,

    'PROB_INFECT': 0.1,
    'PROB_DIE': 0.0001,
    'PROB_CURED': 0.01,
}

สร้างตัว Simulator

ต่อไปเราจะมาสร้างตัว Simulator กันนะครับ โดยตัว Simulator เนี่ย มีหน้าที่วนลูปเพื่ออัพเดตค่าต่าง ๆ ในแต่ละวัน และ monitor status ในแต่ละว่ามีคนสุขภาพดี ติดเชื้อ หรือเสียชีวิตกี่คนแล้ว นะครับ

อันนี้โค้ดในส่วนของการวนลูปเพื่ออัพเดตค่าต่าง ๆ ในแต่ละวันนะครับ จะใช้ method ชื่อ run() และรัน input เป็น จำนวนวันที่จะทำการคำนวณ

class Simulator:
    ...
    def run(self, max_days):
        for self.days in range(1, max_days+1):
            random.shuffle(self.people)

            self.meet_friends()

            for person in self.people:
                person.update()

            self.monitor()
    ...

โดยในแต่ละรอบลูปของ method run() เนี่ย ก็จะทำการ shuffle list ของคนนะครับ เพื่อให้ลำดับของคนใน list แตกต่างกันออกไปในแต่ละวัน จากนั้น self.meet_friends() ก็จะทำการสุ่มคนออกมาและจับให้เจอกันนะครับ

แล้วก็เรียก person.update() เพื่ออัพเดตสถานะของคนนั้น เช่น อัพเดตสถานะจาก ติดเชื้อ เป็น สุขภาพดี หรือ เสียชีวิต

สุดท้ายก็ monitor ค่าต่าง ๆ ในวันนั้น ๆ และเก็บเอาไว้เพื่อไป plot graph ตอนจบนะครับ

อันนี้เป็น method meet_friends() ก็ไม่มีอะไรซับซ้อน แค่วนลูปคนแต่ละคน แล้ว sample คนออกมา เท่ากับ N_MEETINGS ก็คือ sample คนออกมา 10 คน แล้วก็ให้เจอกัน โดยเรียกคำสั่ง person.meet_with(friend)

class Simulator:
    ...
    def meet_friends(self):
        for person in self.people:

            friends = random.sample(self.people, self.config['N_MEETINGS'])

            for friend in friends:
                person.meet_with(friend)
    ...

สร้างคน (Person)

ต่อไปก็จะสร้าง class Person ขึ้นมา โดยสิ่งที่ Person ต้องทำก็จะมี 2 method ที่ต้องเขียน (1) คือ method update() คือใช้ในการ update สถานะว่าหลังจากติดเชื้อ จะให้ติดเชื้อต่อไป หรือหายดี หรือเสียชีวิต ตามความน่าจะเป็นที่เราได้นิยามเอาไว้ใน scenario และ (2) คือ method meet_with() ใช้เป็นตัวแทนของการเจอกัน ของคนสองคนนะครับ โดยถ้าหากคนใดคนหนึ่งมีสถานะเป็น ติดเชื้อ อีกคนจะมีโอกาสติดเชื้อ เป็น PROB_INFECT ครับ

เริ่มจาก method update() มี logic เป็นอย่างนี้ครับ

  1. ถ้าสถานะเป็น เสียชีวิต หรือ สุขภาพดี: ไม่ต้องทำอะไร
  2. สุ่มเลขตั้งแต่ 0 ถึง 1 ถ้ามีค่าน้อยกว่า PROB_DIE (0.0001) จะเปลี่ยนสถานะเป็น เสียชีวิต ก็คือจะมีโอกาส 0.01% ที่จะเสียชีวิตนั้นเองครับ
  3. แต่ถ้าไม่เสียชีวิต: ให้สุ่มเลขตั้งแต่ 0 ถึง 1 ถ้ามีค่าน้อยกว่า PROB_CURED (0.01) จะเปลี่ยนสถานะกลับเป็น สุขภาพดี ก็คือจะมีโอกาส 1% ที่จะหายเป็นปกติ ตามที่เรากำหนดเอาไว้ครับ 
class Person:
    ...
    def update(self):
        if self.is_died or not self.is_infected:
            return

        # random result whether this infected one will die!!!
        if get_binary_random(prob=self.config['PROB_DIE']):
            self.is_died = True

        # random result whether this infected one will be cured!!!
        elif get_binary_random(prob=self.config['PROB_CURED']):
            self.cured()
    ...

ในโค้ดที่ใช้สุ่มเลขผมสร้างเป็น function ชื่อ get_binary_random() มาใช้แทนนะครับ เพราะคิดว่ามันสื่อความหมายมากกว่า ซึ่งตัว function ถูกประกาศเอาไว้อยู่ด้านบนนะครับ ตรงส่วน util สามารถเลื่อนขึ้นไปดูได้ครับ

ต่อไป method meet_with() ครับ การทำงานก็คือ ถ้ามีคนใดคนหนึ่งติดเชื้อ ส่วนอีกคนไม่ติด ก็จะสามารถมีการเพร่เชื้อได้ครับ โดยมีโอกาสแพร่เชื้อเป็น 10%

ในส่วนของเงื่อนไขผมเขียนเป็น condition แบบนี้

        if self.is_infected + other.is_infected == 1:

self.is_infected จะให้ค่าเป็น True หรือ False ครับ ซึ่งถ้าเอามาบวกกัน ใน Python True จะมีค่าเป็นเลข 1 และ False จะมีค่าเป็นเลข 0 ในโค้ดจึงใช้การบวกกันแล้วตั้งเงื่อนไขเป็นเมื่อผลบวกเป็น 1 ซึ่งหมายถึงเมื่อมีผู้ติดเชื้อเป็นคนใดคนหนึ่ง แค่หนึ่งคนนั่นเองครับ

ส่วนในการแพร่เชื้อ ก็ใช้วิธีการสุ่มเลขแบบเดิมครับ ก็คือถ้าค่าสุ่มน้อยกว่า 0.1 สุดท้ายทั้งสองคนก็จะมีสถานะเป็น ติดเชื้อ ครับ

ได้โค้ดเต็ม ๆ เป็นดังนี้

class Person:
    ...
    def meet_with(self, other):
        # condition: one is healthy and the other is sick (XOR)
        if self.is_infected + other.is_infected == 1:

            # random result whether the healthy one will be infected
            if get_binary_random(prob=self.config['PROB_INFECT']):
                self.infect()
                other.infect()
    ...

เท่านี้ก็ได้โค้ดที่ model โครงสร้างของโลกสมมุติ และโรคสมมุติของเราเรียบร้อยแล้วครับ ต่อไปก็มาลอง run จริงกันเลย

ลอง Simulate

เพื่อความสะดวก ผมสร้าง function สำหรับการรัน simulation ขึ้นมา โดยรับ input เป็น dict ของ configuration ที่ต้องการใช้ และจำนวนวันที่ให้รันนะครับ

โดยใน function มีการทำงานดังนี้ครับ

  1. สร้าง Simulator ขึ้นมา
  2. add คนเข้าไปใน Simulator โดยให้ คนจำนวน N_INFECTED_INIT คนแรก มีสถานะเป็นติดเชื้อ (ใน default config ของเราก็คือให้คนที่ 1 เป็นผู้ติดเชื้อนั้นเองครับ)
  3. run simulation 
def simulate(config, max_days):
    simulator = Simulator(config)

    n_population = config['N_POPULATION']
    for i in range(n_population):
        person = Person(config)

        # ทำให้คน N คนแรกมีสถานะ `ติดเชื้อ`
        if i < config['N_INFECTED_INIT']:
            person.infect()

        simulator.add_person(person)

    simulator.run(max_days)

    return simulator

ทีนี้ก็เริ่มลองรันจริงดูเลยครับ โดยใช้ default config ที่เรากำหนดเอาไว้ตอนแรกสุดก่อน เป็นเวลา 30 วัน

simulator = simulate(default_config, 30)

ก็ใช้เวลารันสักพักนะครับ จากนั้น result ของ simulation คือ status ของระบบในแต่ละวัน ซึ่งมาจาก function monitor() สามารถเรียกดูได้แบบนี้ครับ

report = simulator.report
print(report)

ก็จะได้เป็น list ของ dict อันใหญ่ ๆ ออกมา ซึ่งเป็นจำนวนของผู้ที่มีสุขภาพดี จำนวนของผู้ติดเชื้อ และจำนวนผู้เสียชีวิตรวมทั้งหมด ของแต่ละวันนะครับ เพื่อให้ดูง่ายก็จะ plot ออกมาเป็น graph ได้แบบนี้ครับ
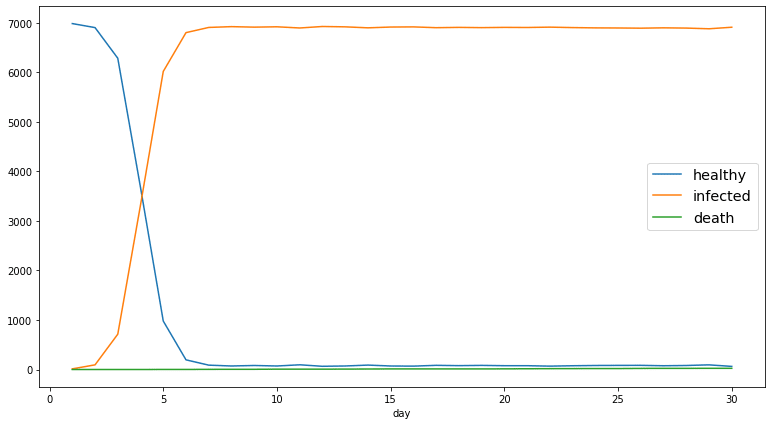
result-default-config.png
ในส่วนของการ plot graph ตรงนี้ ผมใช้ module pandas และ matplotlib นะครับ ถ้าสนใจสามารถศึกษาดูเพิ่มเติมได้ครับ

จะเห็นว่าใน 30 วันแรก จำนวนผู้เสียชีวิตไม่ค่อยเพิ่มขึ้นมาเท่าไหร่ เพราะเรากำหนดให้ความน่าจะเป็นในการเสียชีวิตค่อนข้างต่ำครับ แต่เพียงแค่ประมาณ 6 วันแรก แทบจะทุกคนกลายเป็นผู้ติดเชื้อไปเกือบหมดแล้ว ถ้ากลับไปดูจากข้อมูลดิบ จะเห็นว่าในวันที่ 7 จำนวนผู้ติดเชื้อกลายเป็น 6804 คน จาก 7,000 คน อย่างรวดเร็ว คิดเป็น 97% ภายใน 1 สัปดาห์ โชคดีนะครับที่ไวรัสตัวนี้อยู่แค่ในโลกสมมุติ 5555

สรุปรวมยอดของ DIVOC-91 ใน 1 เดือนแรก เหลือคนสุขภาพดีอยู่ 63 คน เป็นผู้ติดเชื้ออยู่ 6913 คน และเสียชีวิตไปแล้ว 24 คนครับ

ลองเป็นรัฐบาล แล้วแก้ปัญหาดูเองเลย!

คำถามครับ สมมุติว่าเราเป็นรัฐบาลที่ฉลาดครับ รู้ล่วงหน้าตั้งแต่วันแรกละ ว่าในอีก 1 เดือนข้างหน้าจะเกิดอะไรขึ้น แล้วเรามีงบอยู่ก้อนหนึ่ง ถามว่าเราจะทำอย่างไร มี choice ให้ครับ:
1. ลดการรวมกลุ่ม
2. ปรับปรุงการรักษา
3. แจกหน้ากากและเจลล้างมือ

วิธีการเลือกเนี่ย เราก็ต้องวิเคราะห์ดูว่าแต่ละตัวเลือก จะส่งผลกับ parameter ตัวไหนในโมเดล ให้เปลี่ยนแปลงไปอย่างไรครับ

ทีนี้สมมุติมีทีมนักวิจัยเอาข้อมูลของแต่ละตัวเลือกมาให้เพิ่ม เป็นอย่างนี้ครับ
1. ลดการรวมกลุ่ม น่าจะส่งผลให้จำนวนของคนที่เจอในแต่ละวัน (N_MEETINGS) ลดลง จาก 10 คน เป็น 6 คน

2. ปรับปรุงการรักษา จะช่วยให้ผู้ติดเชื้อเนี่ยเข้าถึงการรักษาได้ง่ายขึ้น และช่วยสนับสนุนเครื่องมือแพทย์ต่าง ๆ จะทำให้โอกาสการหายติดเชื้อ (PROB_CURED) เพิ่มขึ้น จาก 1% เป็น 10%

3. แจกหน้ากากและเจลล้างมือ แจกหน้ากากเนี่ยก็จะทำให้เวลาเจอกันมีโอกาสการติดเชื้อต่ำลง และทำความสะอาดด้วยเจลล้างมือก็จะป้องกันไวรัสจากการสัมผัสได้อีก จะทำให้ PROB_INFECT ลดลง จาก 10% เป็น 3% เท่านั้น

ถ้าได้ตัวเลขประมาณแบบนี้ก็สบายแล้วใช่ไหมครับ เราก็สามารถใช้โมเดลที่เรามีมา simulate ดูเอาได้เลย ว่าเมื่อทำแต่ละ choice อีก 30 วัน จะเกิดอะไรขึ้น

ผมสร้าง function ชื่อ try_new_config() ขึ้นมา เพื่อให้สามารถแก้ config และรันได้ง่าย ๆ นะครับ โค้ดข้างในก็คือเอาโค้ดที่เรา simulate และ plot มาต่อกันเฉย ๆ ครับ ไม่มีอะไร

1. ลดการรวมกลุ่ม

N_MEETINGS: 10 -> 6
result-custom-4-2.png
จะเห็นว่าการลดการรวมกลุ่มช่วยชะลอการแพร่เชื้อได้เล็กน้อยครับ สังเกตุได้จากจุดตัดของจำนวนคนสุขภาพดี (สีฟ้า) และจำนวนผู้ติดเชื้อ (สีเหลือง) จะอยู่ที่ประมาณวันที่ 8 ในขณะที่กราฟเดิมของเราจะอยู่ที่ประมาณวันที่ 4 แต่เมื่อผ่านไป 30 วัน จำนวนผู้ป่วยก็ไม่ต่างกันมาก ส่วนจำนวนผู้เสียชีวิตลดลงมาเป็น 19 คน จาก 24 คนครับ

2. ปรับปรุงการรักษา

PROB_CURED: 0.01 -> 0.1
result-custom-4-1.png
ที่น่าสนใจคือจุดพีคของเส้นจำนวนผู้ติดเชื้อ (สีเหลือง) ต่ำกว่ากราฟเดิม ประมาณ 700 คน เนื่องจากผู้ป่วยฟื้นตัวกลับมาสุขภาพดีได้เร็วมากขึ้นนั่นเองครับ

3. แจกหน้ากากและเจลล้างมือ

PROB_INFECT: 0.1 -> 0.03
result-custom-3.png
ผลกระทบที่ดูจากกราฟนี้จะ คล้ายกับมาตรการลดการรวมกลุ่ม คือเป็นการชะลอการแพร่เชื้อออกไป แต่ไกลกว่า ทำให้จำนวนผู้เสียชีวิตต่ำกว่ามาก คือแค่ 9 คน จากเดิม 24 คนครับ ถ้ามองหาการแก้ปัญหาเฉพาะหน้าสำหรับ 1 เดือน วิธีนี้ก็อาจจะไม่เลว

ผลลัพธ์และข้อสรุปที่ได้อาจจะแปลก ๆ ไปสักหน่อย เพราะตัวเลขพวกนี้ผมมั่วขึ้นมาเองทั้งหมดครับ 5555 ทำให้ไม่สามารถนำไปอ้างอิงในโลกความเป็นจริงได้ แต่สำหรับในโลกสมมุตินี้ ถ้าเราเป็นรัฐบาลและตัดสินใจโดยใช้โมเดลและข้อมูลการวิจัย จะเห็นว่าเราสามารถเลือกตัดสินใจได้อย่างมีเหตุมีผล และสามารถรู้หรือทำนายล่วงหน้าได้ว่าทำอะไรไปจะเกิดผลกระทบแบบไหน ก็จะสามารถวางแผนเตรียมการต่อไปได้อย่างมีประสิทธิภาพครับ

ส่วนจะเลือก choice ไหนนั้น ให้ผู้อ่านตัดสินใจเองได้เลยครับ ว่าจะเลือกจากจำนวนผู้เสียชีวิตในระยะสั้น หรือการรักษาในระยะยาว หรือแม้แต่ choice อื่น เช่นเลือกทั้งการรักษาและแจกหน้ากากเป็นต้น ก็สามารถลองเล่นดูได้ใน colab notebook ได้เลยครับ

Summary

ใน part นี้เราก็ได้สร้าง model แบบง่าย ๆ เพื่อ simulate การแพร่กระจายของโรคระบาดไปแล้วนะครับ ซึ่งหลาย ๆ ท่านก็จะเห็นว่าตัว model เอง มีความไม่สมเหตุสมผลอีกมาก เช่น

  • ในแต่ละวัน model ใช้การสุ่มให้คนคนหนึ่งเจอใครก็ได้ แต่ในความเป็นจริงแล้วเราอาจจะไม่ได้มีโอกาสเจอทุกคนบนโลก อาจจะเจอได้เฉพาะคนที่อยู่ในบริเวณใกล้เคียงหรือทำงานที่เดียวกันเท่านั้น นี่อาจจะเป็นสาเหตุให้ DIVOC-91 แพร่กระจายอย่างรวดเร็วเกินจริงครับ
  • ปกติเราอาจจะไม่ได้ออกจากบ้านและเจอคนถึง 10 คนทุกวัน บางวันเราอาจจะแค่ไปจ่ายตลาดแล้วกลับมาบ้านก็ได้
  • model นี้เรายังไม่ได้รวมการแพร่กระจายที่อาจจะเกิดขึ้นได้ จากคนที่อาศัยอยู่ในบ้านเดียวกัน

และอื่น ๆ อีกมาก ซึ่งใน part ต่อ ๆ ไป เราก็จะ implement model ให้ซับซ้อนยิ่งขึ้น เพื่อแก้ไขประเด็นดังกล่าวกันนะครับ

สุดท้ายนี้ ย้ำอีกสักเล็กน้อยว่าอยากให้มอง project นี้เป็น OOP project แบบขำ ๆ นะครับ ผลลพธ์จาก model ที่เราลองรันเล่นกันในนี้ไม่สามารถเอาไปสรุปหรือแย้งการตัดสินใจของเจ้าหน้าที่จริงที่มีความรู้เฉพาะทางและข้อมูลที่แม่นยำได้นะครับ

note: ในการวิเคราะห์โดยทั่วไป เพื่อให้คำนวณได้อย่างมีประสิทธิภาพ ปกติก็จะต้อง formulate ออกมาเป็นโมเดลคณิตศาสตร์ และ derive ออกมาเป็นสมการ จะสามารถคำนวณผลลัพธ์ ณ จุดเวลาใด ๆ ได้เร็วกว่า แต่ใน project นี้ตั้งใจจะเขียนเป็น OOP project ครับ และใน part สุดท้ายก็คิดว่าจะ visualize ออกมาภาพเคลื่อนไหวสั้น ๆ อันหนึ่ง ให้เห็นเป็นตัวคนวิ่งไปวิ่งมาจริง ๆ ก็น่าจะสนุกดีครับ

และถ้ามีเรื่องไหนที่สนใจเพิ่มเติมสามารถ comment เอาไว้ได้นะครับ

FB Page: Copy Paste Engineer

- ขอบคุณที่อ่านครับ -

Top comments (0)