Um resumo sobre: algoritmos de ordenação.

Introdução.
Após a construção de uma base de dados, pode ser necessário a ordenação dessas informações. Essa ordenação pode ser nomes em ordem alfabética, endereço pelo cep, vendas por preço, cidades em ordem crescente de população e etc. Ter esses dados ordenados faz com que tenhamos performance na pesquisa de dados, por exemplo, escolhendo a pesquisa binária O(log n), no lugar da linear O(n). Você pode saber mais sobre pesquisa linear e binária com este link e notação Big-O, para entender sobre a comparação da complexidade de algoritmos pela entrada que ele recebe, neste link.
Sempre bom termos em mente, quando pensamos em dados, é pensar na inserção, exclusão e pesquisa dos dados. Se por um lado a pesquisa de dados em vetores ordenados é mais performática que em vetores não ordenados, pela possibilidade que realizar a pesquisa binária, por outro lado, em vetores ordenados, a performance para inserção de dados pode não ser tão boa quanto em vetores não ordenados, uma vez que para inserir em um vetor ordenado, iremos precisar pesquisar onde o dados irá ser inserido e deslocar os demais dados para que o elemento em questão ocupe a sua devida posição.
Aí entra a estrutura de ordenação de dados, para inserirmos com a agilidade dos vetores não ordenados e pesquisarmos com a rapidez dos vetores ordenados. Para entendermos como funcionam esses algoritmos de ordenação, iremos ver: bubble sort (bolha), selection sort (seleção), insertion sort(inserção), shell sort, merge sort e quick sort.

Bubble Sort (bolha).
O mais lento e simples de todos os algoritmos de ordenação.
Ele funciona da seguinte maneira:

• Compara dois números, se o da esquerda for maior, os elementos devem ser trocados, sendo que o menor se desloca uma posição à esquerda.
• À medida que o algoritmo avança, os itens maiores “surgem como uma bolha” na extremidade superior do vetor.

Com este link podemos ter uma excelente noção de como funciona esta estrutura de ordenação com o passo a passo (é muito importante acessarem o último link para ver o algoritmo em funcionamento). Em uma visão geral, caso tenhamos um vetor com 10 elementos, o algoritmo fará 9 comparações na primeira rodada, 8 na segunda, 7 na terceira e assim por diante. Neste caso, ele fará 45 comparações. O Big-O dele será quadrático O(n²), sendo assim, o algoritmo irá comparar, aproximadamente, (n² / 2) comparações. Nós dividimos por 2, pois é uma média. No caso de 10 elementos, dará aproximadamente 50 passos. Nesse caso, foram exatamente 45 passos, pois o valor é aproximado. Em 99% das vezes temos mais comparação do que trocas de fato dos valores, uma vez que os valores só serão trocados quando houver necessidade.

Aqui está um algoritmo feito em python utilizando a ideia de bubble sort:

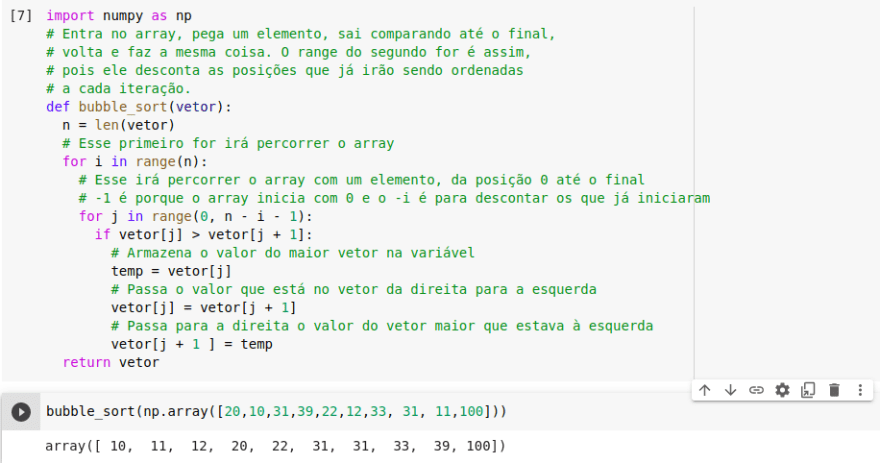
Selection Sort (seleção):
Melhora a ordenação do método da bolha, uma vez que a selection sort reduz o número de trocas necessárias, reduzindo de N² para N. Entretanto, o número de comparações permanece N².
Esta estrutura funciona da seguinte maneira:

• Percorre todos o elementos e seleciona o menor;
• O menor elemento é trocado com o elemento da extremidade esquerda do vetor(posições iniciais);
• Os elementos se organizam à esquerda, diferente da bolha que organiza seus elementos à direita.

Neste link, você selecione o selection sort e assista calmamente como ocorre o processo. Repare que o algoritmo faz a varredura e marca o menor valor com a cor vermelha. Ao final do processo, o menor se deslocará para o início.
Em uma visão geral, caso tenhamos um vetor com 10 elementos, funcionará da mesma maneira que o bubble sort na COMPARAÇÃO:

• O algoritmo fará 9 comparações na primeira rodada, 8 na segunda, 7 na terceira e assim por diante. Neste caso, ele fará 45 comparações. O Big-O dele será quadrático O(n²), sendo assim, o algoritmo irá comparar, aproximadamente, (n² / 2) comparações. Nós dividimos por 2, pois é uma média. No caso de 10 elementos dará aproximadamente, 50 passos. Nesse caso, foram exatamente 45 passos, pois o valor é aproximado. Aqui está a grande diferença entre o bubble sort e o selection sort: enquanto o bubble sort precisará de 3 passos vezes o número de trocas sendo que no pior dos casos no selection, nós iremos realizar 10 passos.

Aqui está um algoritmo feito em python utilizando a ideia de Selection Sort:

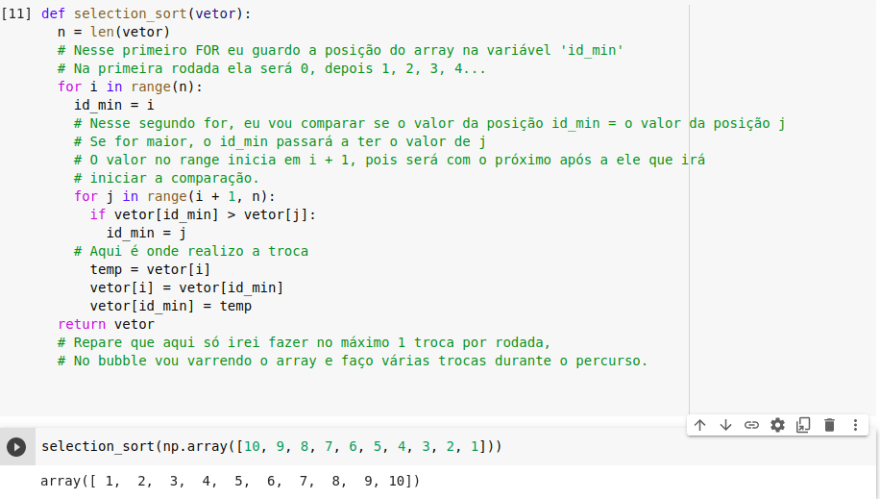
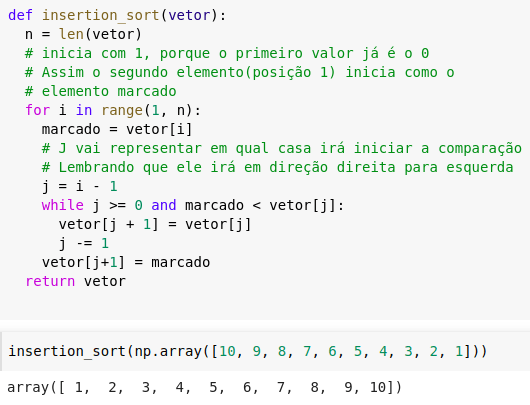
Insertion Sort:
Essa é a ordenação por inserção, sendo duas vezes mais rápida do que a bubble sort e um pouco mais ágil que a selection sort. Em questão de funcionamento, ela age da seguinte forma:

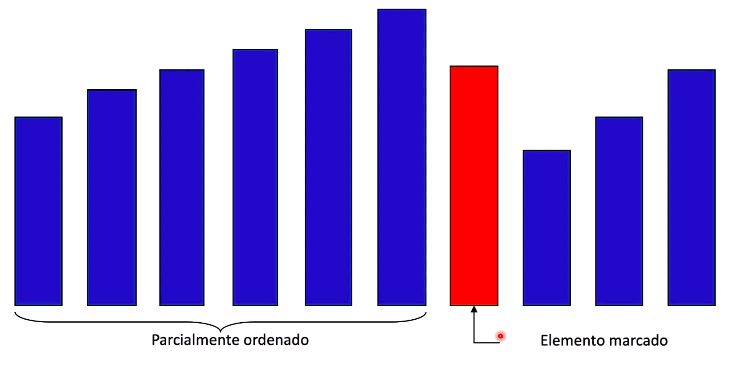
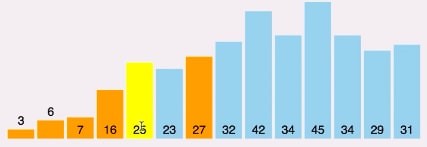
• Há um marcador no meio do vetor;
• Os elementos à esquerda estão parcialmente ordenados (ordenados entre eles, porém não estão na posição final);
• Os elementos à direita do marcador não estão ordenados;

Repare que o vermelho é a posição marcada do vetor. Ele irá procurar a posição que ele irá ocupar à direita:

Repare que o elemento vermelho foi inserido e agora o elemento marcado é o verde:

Com este link você clica em insertion sort e veja como funciona este algoritmo de ordenação.
Para esta estrutura, faremos as seguintes análises:

• Para dados que já estão parcialmente ordenados, esta estrutura de ordenação pode ser mais eficiente que as outras apresentadas até aqui;
• Se os dados estiverem em ordem inversa, esse método é mais lento que o método da bolha;
• Em termos de comparação dos dados, este tem uma média de metade dos passos das ordenações bubble e selection.

Aqui está um algoritmo feito em python utilizando a ideia de Insertion Sort:

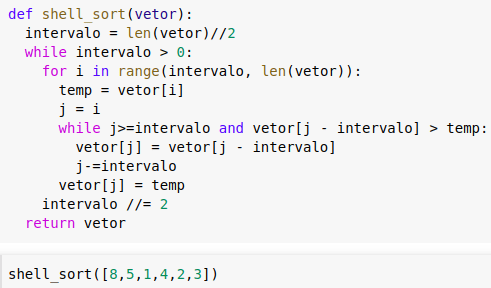
Shell Sort (Shell -> pesquisador que inventou esse de algoritmo)

Este algoritmo melhora a ordenação do insertion sort, assim, podemos dizer que é uma versão melhorada do insertion.

Ele funciona da seguinte maneira:

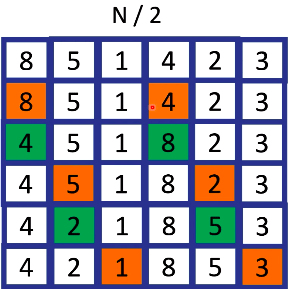
• O vetor original é quebrado em subvetores;
• Cada subvetor é ordenado comprando e trocando os valores;
• No final da rodada esse subvetor é quebrado em mais um subvetor. Observe nesta imagem:

O vetor é dividido no meio. Pegou a posição 0, pulou duas posições e pegou a posição 3. Ele compara os valores e joga o menor para a esquerda e o maior para a direita. Em seguida, pula uma casa, o que estava no 0 vai para o 1 e o que estava no 3 vai para o 4, em seguida faz novamente a comparação. Esse procedimento segue até terminar. Após isso, ele é quebrado novamente no meio.

Neste link você terá uma melhor noção de como funciona este algoritmo de ordenação.

A complexidade deste algoritmo dependerá dos intervalos escolhidos, sendo que o pior caso será O(n²) e o melhor caso O(n * log n). Lembrando que o melhor caso do selection sort é O(n²) e do bubble sort é O(n²)

Merge Sort(juntar):
Um dos algoritmos de ordenação mais populares, o merge sort funciona da seguinte maneira:

• Ele segue a premissa de dividir para conquistar, com isso, ele divide a lista diversas vezes até ter um único elemento;
• Após dividir ao máximo, ele vai juntando(merge) e ordenando.

Veja o fluxograma para uma melhor visualização:

Em relação a notação Big-O, no pior e no melhor caso são O(n* log n). Em comparação com o bubble sort e o selection sort, o merge sort é melhor, uma vezes que os outros são O(n²) e o shellsort, no pior caso é O(n²) e no melhor é O(n*log n).

Esse algoritmo feito em python exemplifica o modelo merge sort:

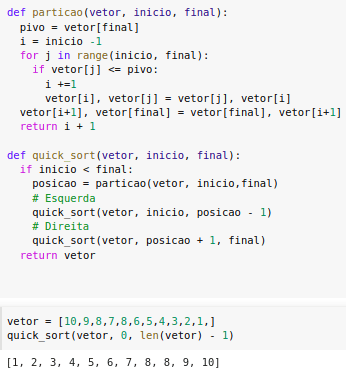
Quick Sort:
É um algoritmo rápido e eficiente criado em 1960, sendo que seu funcionamento consiste da seguinte forma:

• O vetor é dividido em sub vetores e é chamado recursivamente para ordenar os elementos;
• Utiliza a estratégia da divisão e conquista.

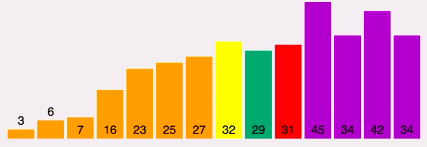
Esse algoritmo possui um conceito de elemento pivô, sendo que a cada rodada ele compara esse elemento com os demais da lista. O elemento que inicia como pivô é o da posição 0. Na comparação, os elementos menores são dispostos do lado esquerdo e os maiores do lado direito, após a comparação o pivô toma a posição do meio, sendo que os maiores ficarão à direita e os menores à esquerda.

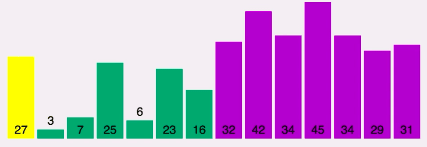
Repare que neste vetor, o pivô é o número 27 e os elementos verdes são menores e os roxos estão à direita:

Agora o 27 toma a posição do meio, trocando com o 16 que está na última posição entre os menores:

Agora o 27 é o final da lista e o 16 será o pivô, repare que agora todos os números maiores que o da posição 6 são maiores que o 16 e lembre-se que ele irá medir até o 27, porque os acima são obrigatoriamente maiores:

Agora o 16 irá trocar com o 6 e o 16 passará a ser o final e o 6 passará a ser o pivô:

Depois de realizar as comparações, o 6 irá trocar de lugar com o 3 e do 3 até o 15 já está ordenado e o 25 passará a ser o pivô:

Depois do reajuste do 25, terminamos a parte da esquerda. Agora iniciamos a parte da direita com o pivô como 32 e assim ficará depois das comparações:

Assim irá até o final. Para uma melhor visualização, acesse este link e clique no botão quick sort.

O pior caso dessa ordenação será O(n²) e o melhor caso O(n * log n).

Aqui está um algoritmo de ordenação quick sort feito em python:

Caso tenha alguma sugestão sobre o tema, mande mensagem. Será muito bom evoluir com sua ajuda! Obrigado por chegar até aqui e espero ter ajudado!

Este resumo é baseado no curso: Estruturas de dados e algoritmos em python