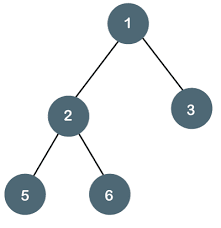
 Binary Trees are hierarchical data structures in which each parent node has at most 2 children nodes. In today's article, we will go over an important topic that shows up in plenty of technical coding interviews.
Binary Trees are hierarchical data structures in which each parent node has at most 2 children nodes. In today's article, we will go over an important topic that shows up in plenty of technical coding interviews.
PROBLEM STATEMENT: Given the root of a binary tree, return the preorder traversal of its nodes' values. Provide an iterative solution instead of a recursive one.
SOLUTION:
Pre-Order Traversal in a Binary Tree happens in this order:
- Visit the root first
- Traverse the left subtree
- Traverse the right subtree
In order to solve this problem with an iterative solution, we will have to implement the Stack data structure. This is a non-linear data structure in which the operations are carried out in a LIFO(Last In First Out) order. The approach to our answer is simple and will be as follows:
- We will initialize two lists i.e one to carry the output and another to act as our stack data structure. The stack will be initialized with the root value of the binary tree.
- We will then perform a while loop on our stack for as long as it has a value. In the loop, the following operations shall be carried out in order:
- Remove(pop) the top most value(the root node) in the stack and append it to the output list
- Push the right child of the popped value into the stack
- Push the left child of the popped value into the stack
- Return the output list at the end of the loop
As a result of this process, the root value will be accessed first, then the left subtree, and then the right subtree values will be accessed last.
It is important to note that the right child is pushed into the stack first then the left child. This is because of the LIFO nature of the stack. Doing so will allow us to access the left child first before the right child.
TALK IS CHEAP, SHOW ME THE CODE:
# Definition of a Binary Tree node
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
output, nodestack = [], [root]
while nodestack:
node = nodestack.pop()
if node: # preorder: root -> left -> right
output.append(node.val)
nodestack.append(node.right)
nodestack.append(node.left)
return output
If this piece was helpful, please feel free to like and subscribe to my newsletter for more DSA content in Python.


Top comments (0)