Previous Day I discuss about the basic components of searching like state space,agent,actions,state etc.Now I tell about the different searching algorithm learning experience from the tutorial.
The problem for searching is used maze path finding you can consider it as environment and a agent let's say A which want to find path from the maze.
Depth First Search(DFS) and Breadth First Search(BFS):
First algorithm I see is DFS or depth first search which i love most because of it going deep to find results.It is using stack data structure to store all the visited nodes or path/decision point and it is going deep until get the dead end after that it will come back to the previous point where it started in this way it find the path from start to destination of a maze.
#####B#
##### #
#### #
#### ##
##
A######
It is a sample maze and applied DFS we got the path like this
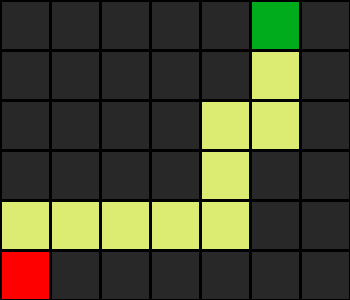
The blacks are the wall and green is the end point and red is the agent ,yellow blocks are the search path by agent.
It is a simple maze if I make it some more complex then:
### #########
# ################### # #
# #### # # # #
# ################### # # # #
# # # # #
##################### # # # #
# ## # # # #
# # ## ### ## ######### # # #
# # # ##B# # # #
# # ## ################ # # #
### ## #### # # #
### ############## ## # # # #
### ## # # # #
###### ######## ####### # # #
###### #### # #
A ######################
Now it will have a red blocks appears it is the explored path by agent using DFS and it come back to the previous point.

Now here is a concept called path cost which is little higher like 194 but we can achieve it optimally if we apply BFS or Breadth First Search.Where DFS work on going deep until get a end but bfs go to wide to wider to search the path.
You can compare DFS as a drill where BFS kind of octopus which use it tenticles to make more area it can cover for above maze bfs is a optimal choice.
Now the problem is solved in much low cost like 77 of total path cost which is much more optimised.But in some time bfs is not enough.
I put a video how bfs and dfs works.
Dfs working
Bfs working
Now to optimise more we are going to know about two types of searching in search in AI.
- informed search: Where we have some information about the environment and we can use it to make the more optimised solving problem.
example:The maze problem if we have the destination point coordinate and source point coordinate we can compare them to get the distance between them in this way we can know how far are we from the source.
- uninformed search: This is just search where agent don't have any information about the environment. It just exploring to get the goal which sometimes useful where we have no information.Previously bfs and dfs example of uninformed search.
Greedy Best First Search:
For informed search we have Greedy Best First search or GBFS where we search the path in the maze by getting the distance of the agent location and destination path determined by a heuristic function h(n). As its name suggests, the function estimates how close to the goal the next node is, but it can be mistaken. The efficiency of the greedy best-first algorithm depends on how good the heuristic function is. For example, in a maze, an algorithm can use a heuristic function that relies on the Manhattan distance between the possible nodes and the end of the maze. The Manhattan distance ignores walls and counts how many steps up, down, or to the sides it would take to get from one location to the goal location. This is an easy estimation that can be derived based on the (x, y) coordinates of the current location and the goal location.
It can be simplified by this:
f(n) = h(n)
Now next it has some comlication/disadvantages like
- It can behave as an unguided depth-first search in the worst case scenario.
- It can get stuck in a loop as DFS.
- This algorithm is not optimal.
A* search
So to solve the unguided path problem I learn another one which use same heuristic function with a evaluation function.
It's called A* search algorithm.
It uses h(n) distance from source to destination and g(n) evaluation function to get the cost of the path taken.
he cost that was accrued until the current location. By combining both these values, the algorithm has a more accurate way of determining the cost of the solution and optimizing its choices on the go. The algorithm keeps track of (cost of path until now + estimated cost to the goal), and once it exceeds the estimated cost of some previous option, the algorithm will ditch the current path and go back to the previous option, thus preventing itself from going down a long, inefficient path that h(n) erroneously marked as best.
Yet again, since this algorithm, too, relies on a heuristic, it is as good as the heuristic that it employs. It is possible that in some situations it will be less efficient than greedy best-first search or even the uninformed algorithms. For A* search to be optimal, the heuristic function, h(n), should be:
Admissible, or never overestimating the true cost, and
Consistent, which means that the estimated path cost to the goal of a new node in addition to the cost of transitioning to it from the previous node is greater or equal to the estimated path cost to the goal of the previous node. To put it in an equation form, h(n) is consistent if for every node n and successor node n’ with step cost c, h(n) ≤ h(n’) + c.
A visualisation of A* search.
I put this part here and next part will coming soon.
Keep exploring,keep learning.
Reference:
Thank you.




Top comments (0)