Early in the history of computers, input/output operations were particularly slow – even in comparison to processor speeds of the time. It made sense to reduce expensive read operations by a form of manual caching by creating either static lookup tables (embedded in the program) or dynamic prefetched arrays to contain only the most commonly occurring data items.
I began watching the Nordic.js 2016 “If you know map I will teach you monads” talk by the amazingly good Mattias Petter Johansson. His educational style is engaging and funny, and helps clearing up some missed realizations while thinking about monads these past two days. I am well into the 95th day territory of my 100 days of code with Haskell currently being stationed in a bluish cosmic nebula thinking about functional computational flow of data. The nebula is made out of lambda pure functions, and monads are everywhere, covered with natural glow.. Anyway the whole talk converges into these two definitions, roots from which the structure of the talk is built.
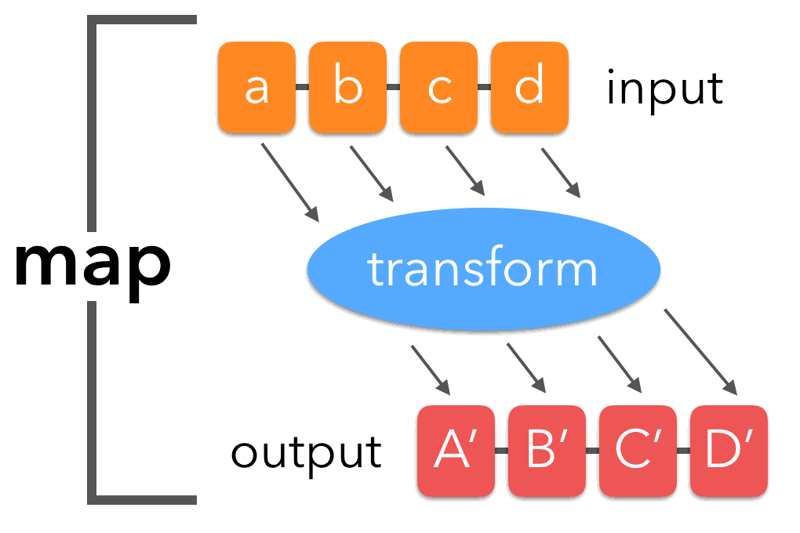
In many programming languages, map is the name of a higher-order function that applies a given function to each element of a functor, e.g. a list, returning a list of results in the same order. It is often called apply-to-all when considered in functional form.
So what is a map, or what kind of an action does mapping represent, what does it mean to map something? There is a very nice wiki page on mapping, the essence of it seems to me that map is an action just doing the application of some designed, provided action, essentially a function, to all the elements in some set, or all the functions in some set, these functions being some kind of transformations, or morphisms. Now what is really interesting is that we could also say that mapping is a map of equivalent relations between two sets, producing a value, a unique value. There are more frames when thinking about maps, for instance the three dimensional planet Earth transforming itself into a two dimensional map by the process of mapping each point of it into a sheet of paper, then maybe like as a stream of actions, like gathering -> preparing -> eating, or mapping all the tones of a musical composition into positions on a guitar fretboard, a two dimensional matrix of six string rows and nineteen fret columns. For instance, a string of tones, represented as western musical notes, a melody of three notes such as C, D, E could be translated or transposed to use the musical term, shifted to a position higher by let's say a third, meaning we would raise each note by three notes. So map (+3) (C, D, E) -> C+3, D+3, E+3
We hear that arrays, streams, trees and promises are all functors.
So I look up the wiki page about array data structure and there’s this lookup table term I have seen together with Haskell, lookup tables being like pure functions since they always provide us with the information we ask, like looking into a dictionary that is alphabetically sorted we get information by looking up words. These words usually , I remember listening to Milewski category theory lectures where he talks about pure functions as lookup tables, and also Peyton Jones giving a talk on Microsoft Excel and how it relates to functional programming. The modern term seems to be a spreadsheet instead of a lookup table, a working analogy that we can study.
It is strangely familiar, then deeply intuitive he notion of a lookup table. I remember studying, memorizing my multiplication table from elementary school. It had all the numbers from 1 to 12, at least that is as far as I could imagine it, meaning it felt like I could only hold within my mind, actually see the two dimensional matrix, the whole field up to number 144. Then I realized there were some repetitions, some numbers that somehow differentiated themselves from the whole field:
- these were like numbers multiplied with number 1, they never changed,
- then geometric patterns such as
6 * 6 = 36
Then I seemed to remember these much faster, having placed them in a lookup table within my own mind.









Top comments (0)