This article is transcribed from Bartosz Adamczewski’s video on LevelUp’s Youtube channel about 5 (Extreme) Performance Tips in C#.
This transcription is made on behalf of ByteHide, we have no association with the author, we just found it super interesting, the team thanks him.
In this article, you will learn 5 different performance tricks that you can do in C#.
They are called EXTREME because, personally, I have not found information like this on the Internet. Yes, there are different performance tricks, but not the ones I’m going to show you here.
Let’s start with a very simple example where we’re gonna have a sum of odd elements, so what we can do here is we can take the array element and they we can check if it’s divisible by two and, if it’s not, then we’re gonna add that element because that element is odd and we can turn the result.
private static int SumOdd(int[] array)
{
int counter = 0;
for (int i = 0; i < array.Length; i++)
{
var element = array[i];
if (element % 2 != 0)
counter += element;
}
return counter;
}
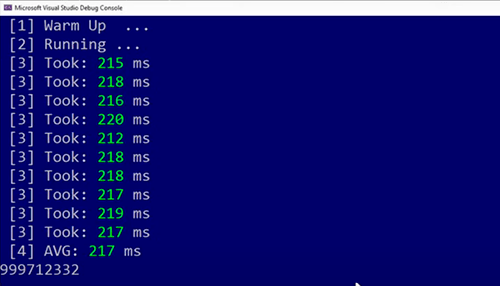
So, if we run it in our simple measuring procedure this is going to take quite a while to compute because we’re going to compute it on 40 million elements, so the average result is around 240–250 milliseconds.
If we look at this function…
Is there something that we can do in order to be to actually optimized? 🤔
It’s there a way for us to have a faster version of this function turns out that there is? 🤔
1. Bit Tricks
We can replace more expensive elements with least expensive elements and in this case I’m talking about the modulus operation. Turns out that the modulus operation can be extremely expensive but the good news is that the jit compiler automatically uses a shift left on the module, so already we have a better implementation but, we can still do better because we have a proper context that the compiler doesn’t and there is a way to make it even faster.
sum = SumOdd_Bit(array);
What we can do is we can do a and operation with one and that will effectively test if our element is out and if it’s odd it’s going to be reduced to just a single value one.
private static int SumOdd(int[] array)
{
int counter = 0;
for (int i = 0; i < array.Length; i++)
{
var element = array[i];
if ((element & 1) == 1)
counter += element;
}
return counter;
}
Now we can check is if this got faster 👇
Now it takes slightly faster because it’s 217 milliseconds from 240 milliseconds* and we got a improvement.
2. Branch Elimination
We can do a branch-free version of that some odd function. We can do it because we already had a kind of an operation that did it because this element and one operation will return one if the element is odd, otherwise it’s going to return zero. That already allows us to eliminate the branch and we can do a multiplication or by the element.
sum = SumOdd_BranchFree(array);
If this is one that means the element is odd, we’re gonna multiply that by one. We’re gonna have an element, otherwise, we’re just going to multiply by zero and have zero. Branch elimination is interesting for a two of reasons:
First of all, there’s certain data sets and data workflows that you can have in an application where the data is very extreme that the branch predictor cannot do a good enough job well.
The second reason is because you want to have a stable performance, because like i said, branch prediction depends on the data and you can have super fast function because you have predictable data but, on the other that might get a bit slower. That’s why you might want to consider that.
Of course you have to keep in mind that branch prediction is expensive, because all of the things that you have to do to eliminate the branch can be expensive like bit hacking tricks.
private static int SumOdd_BranchFree(int[] array)
{
int counter = 0;
for (int i = 0; i < array.Length; i++)
{
var element = array[i];
var odd = element & 1;
counter += (odd * element);
}
return counter;
}
Let’s check the performance 👇
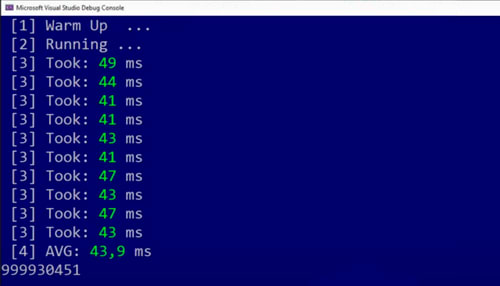
It took 43 milliseconds which is a big improvement from 217 milliseconds and that’s really good.
3. Instruction Parallelism
Since we did branch elimination already, what we can do now is we can do a instruction level parallelism here. Instruction level parallelism means that modern cpus usually can do multiple things at the same time provided that there’s no data hazards between different sort of elements and that these instructions that they execute can really be executed on multiple ports.
sum = SumOdd_BranchFree_Parallel(array);
We effectively duplicated our counter to not have data hazards and now we can do certain operations at the same time, for example: and operation can be done four times per one cpu cycle and in order to be able to figure out if you can benefit from these improvements.
private static int SumOdd_BranchFree_Parallel(int[] array)
{
int counterA = 0;
int counterB = 0;
for (int i = 0; i < array.Length; i += 2)
{
var elementA = array[i];
var elementB = array[i + 1];
var oddA = elementA & 1;
var oddB = elementB & 1;
counter += (oddA * elementA);
counter += (oddB * elementB);
}
return counterA + counterB;
}
Let’s test the performance of this version 👇
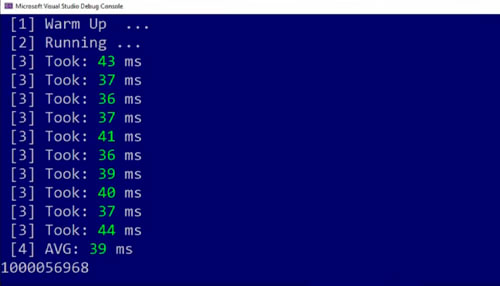
Now 39 milliseconds. It’s slightly faster but only slightly and the reason might be that we had a multiplication here.
4. Bounds Checking
Tip number four would be to eliminate all of the bounce checks, because the previous method had a lot of bounce checking of the array, although, we sort of fulfill almost the correct signature not to have any bounce checks but, if we’re going to change the signature of i, we’re gonna get two elements of the array.
sum = SumOdd_BranchFree_Parallel_NoChecks(array);
There are a couple of ways of eliminating them but, one of them that’s the simplest one it’s not the best one mind you. Is to just have a fixed pointer to that array and then, basically, we’re gonna convert that to the end pointer and gonna we’re gonna take that pointer and access the elements.
private static int SumOdd_BranchFree_Parallel_NoChecks(int[] array)
{
int counterA = 0;
int counterB = 0;
fixed (int* data = &array[0])
{
var p = (int*)data;
for (var i = 0; i < array.Length; i += 2)
{
var elementA += (p[0] & 1) * p[0];
var elementB += (p[1] & 1) * p[0];
p += 2;
}
return counterA + counterB;
}
Let’s measure the performance of this version 👇
Better, 32 milliseconds from 39 milliseconds. We got a improvement.
5. Maximize Ports
This tip would be, if we know all of these things now, we can do a better job with ports. We can get another pointer to our data and the first pointer is going to be loaded to registers but the second won’t be. That effectively eliminates the need to have just a single multiplication per operation.
sum = SumOdd_BranchFree_Parallel_NoChecks_BetterPorts(array);
Although, we’re still constrained by loads as we can do only two loads per cycle and we have eight loads here, still the multiplication would be the term the the biggest factor in performance degradation here and we can check if this is really true.
private static int SumOdd_BranchFree_Parallel_NoChecks_BetterPorts(int[] array)
{
int counterA = 0;
int counterB = 0;
int counterC = 0;
int counterD = 0;
fixed (int* data = &array[0])
{
var p = (int*)data;
var n = (int*)data;
for (var i = 0; i < array.Length; i += 4)
{
counterA += (n[0] & 1) * p[0];
counterB += (n[1] & 1) * p[1];
counterC += (n[2] & 1) * p[2];
counterD += (n[3] & 1) * p[3];
p += 4;
n += 4;
}
return counterA + counterB + counterC + counterD;
}
Let’s check it out and let’s run this version👇
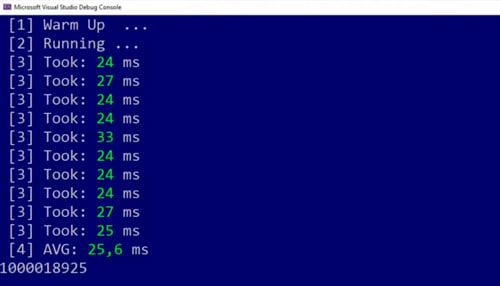
It took 25.6 milliseconds which is the fastest version.
Just to show you in how it looks in a nice graph, you can see the ports version is slightly faster than the no checks with four parts version and from the first tip to the last tip we have a performance benefit by almost a factor of 10.






Top comments (11)
This article is copied wholesale from my youtube video: youtube.com/watch?v=Tb2Fx9qku_o
If you're going to copy all of the things 1to1, then at least you should credit the author.
Overall a good article, but the example code has a lot of bugs. So it is hard to know if what is shown was used for your performance tests. If it was then your speed improvements may have more to do with optimizations for invariants. For instance in #3 you add to “counter”, but return the sum of counterA and counterB which are both zero. Similar issue in #4, and it also uses the wrong value for the B portion (you’re using p[0] for both A and B sums.
Found how to eliminate multiplication. It makes the code just a little bit faster compared to SumOdd_BranchFree but this technique performs worse than multiplication methods with parallel execution.
The code is the following:
Here's one more option to consider. It's twice as fast as the best one above and uses the bitwise step in actual parallel processing. It probably could have further optimizations from above incorporated into it also. With this you'd call ParallelLoop(array, numberOfTasksYouWantForYourMachine).
Also, I had never thought of bit checking before and have always used mod. I will certainly use this in the future. Nice article!
private static long AddViaGap(long[] array, int gap, int offset) {
long counter = 0;
for (int i = offset; i < array.Length; i += gap) {
var element = array[i];
var odd = element & 1;
counter += (odd * element);
}
return counter;
}
private static long ParallelLoop(long[] array, int taskCount) {
var tasks = new Task[taskCount];
for (var counter = 0; counter < taskCount; counter++) {
var currentCounter = counter;
tasks[counter] = Task.Run(() => AddViaGap(array, taskCount, currentCounter));
}
Task.WaitAll(tasks);
return tasks.Sum(o => o.Result);
}
Good tips, thanks. Not strong on C# myself but surely you've introduced a bug at stage 3, e.g. if your array has an odd length? I.e. elementB won't exist.
You could get rid of the multiplication by defining a array with length 2.
First entry at Index 0 is 0
Second entry at index 1 is -1
Instead of multiplying value by 1 or 0, you could simply do a Bitwise AND Operation with the value at Index 1 or 0.
great article! thanks for sharing!
Nice article.
☕☕☕☕☕
🔒🔒🔒🔒🔒
Some comments have been hidden by the post's author - find out more