열기
여러 프로그래밍 언어에서 함수형 프로그래밍을 지원한다. 이러한 방식은 람다 대수가 이론적 근간이 된다고 하는데, 어떤 내용인지 궁금하므로 매우 짧게 이런 식이구나 까지만 알아보도록 한다.
정의
튜링 머신과 같이 어떤 계산가능한 함수도 표현할 수 있지만, 하드웨어보다는 소프트웨어적인 접근을 취하고 있다.
기본 용어는 name, expression이다. Name은 흔히 말하는 variable이라고 생각하면 되고 알파벳 문자로 표현된다. Expression은 아래와 같이 재귀적으로 표현된다.

따라서 표현식(expression)은 변수(name)이거나 함수(function)이거나 적용(application)이다. 함수(function)는 λ 키워드로 함수임을 알리고 인자(argument)로 변수와 본문(body)로 표현식을 써서 정의한다. 적용(application)은 표현식 하나를 다른 표현식에 적용시킨다는 의미로 이 자체가 표현식이다. 키워드는 점(.)과 람다기호(λ) 2가지 밖에 없다. 가독성을 위해 괄호를 사용할 수 있다.
간단한 함수(function)의 예로 항등 함수(identity function)가 있다.

바(|) 왼쪽은 람다 표현, 오른쪽은 이해를 돕기 위한 코틀린 코드에서의 표현이다(이제 코틀린 기초 문법 보는 중이라 틀렸을 수도 있음). 첫번째 x는 이 함수의 인자(argument)를 나타내고, 두번째 x는 함수의 본문(body)를 나타낸다. 즉 자기자신을 반환하는 함수이다. 일단 여기에서 람다 함수에는 sin(), sum()과 같은 이름이 없다는 것을 알 수 있다.
함수를 표현식에 “적용”할 수 있다. 실제로 표현식을 함수에 대입하지만 반대방향으로 표현한다.
가장 간단한 “적용”은,

이 경우 표현식 x가 함수라고 가정한 경우이다.
항등 함수로 적용의 예를 들면,
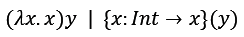
위 적용(λ(x.x))은 인자 x를 변수값 y로 대체하고 본체를 반환하기 때문에 결과는 y이다.

변수는 단지 값을 담는 place holder 역할이므로 x, y, z 등 어떤 이름으로 지어도 상관없다. 즉,

자유 변수(free variable), 종속 변수(bound variable)
위키백과 설명을 보자 (왠지 이해하기 더 어려워졌다):
논리학과 컴퓨터 과학에서, 자유 변수(自由變數, 영어: free variable)는 수식 속의 변수 가운데 상숫값으로 치환할 수 있는 것이다. 반대로 종속 변수(從屬變數, 영어: bound variable)는 상숫값으로 치환하였을 때 수식이 본래의 의미를 잃게 되는 변수이다.
람다 함수의 예를 보자.
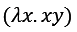
함수 본문에 있는 변수가 인자에도 있으면 종속되었다고 하고, 그렇지 않으면 자유라고 한다. 따라서 x는 종속 변수이고, y는 자유 변수이다. 주의할 점은 변수 이름은 scope이 함수 하나에 한정된다는 것이다. 이름이 같더라도 옆 함수에서는 사실 다른 변수이다.

첫번째 표현식 (λx.x)에서 x는 종속 변수이고, 두번째 표현식 (λy.xy)에서 x는 자유 변수이며, 각 표현식의 x는 전혀 다른 변수이다.
치환
항등 함수에 항등 함수를 “적용”시킨다면 치환을 이용하여 그 결과를 추론할 수 있다. 위에서 설명했듯이 변수 이름은 함수들을 걸쳐서는 의미가 없으므로 치환하면,
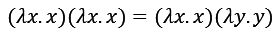
앞 람다 함수 인자에 뒤의 표현식을 대입하면,

위 함수는 인자와 같은 것을 반환한다는 정의이므로 결과는,

즉 다시 항등 함수가 된다.
연습 문제1: (λx.(λy.xy))y를 치환하면?
풀이1: scope은 다른데 이름이 같은 변수들이 헷갈리므로 먼저 치환해서 모호함을 없앤다.
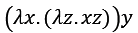
맨 오른쪽 y 변수를 인자 x로 치환해서 본체를 반환한다.

연습 문제2: (λx.(λy.(x(λx.xy)))y를 치환하면?
풀이2: 대입할 맨 오른쪽 y와 람다 함수 본문의 y는 서로 다른 변수이므로 본문 쪽을 치환

변수 y를 왼쪽 람다 인자로 치환해서 본문을 반환하면,

산술 연산
람다 대수에서는 모든 것이 함수라 숫자를 표현할 방법이 필요했다. 음이 아닌 정수 체계를 표현하고자 한다면, (1) 시작값(0)과 (2) 다음 값을 구하는 함수(successor), 두 가지만 있으면 구축할 수 있다. 시작값인 zero를 아래와 같이 정의했다(이게 도대체 왜 0이냐는 의문이 생기지만).
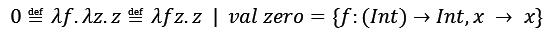
Zero는 함수 f(successor)와 변수 z(양의 정수)를 입력으로 받아 다시 변수 z를 반환하는 함수로 정의했다.

2, 3, … 모두 기본값에 successor 함수를 몇 번 적용했는지로 정의된다.
덧셈의 경우에도 함수로 정의되는데, 인자 (a, b)를 받아서 zero에 successor를 a번 적용하고, 그 결과에 다시 successor를 b번 적용한다.
마무리
여기까지가 보통 람다 대수 책의 앞 부분이다. 우리의 목적은 대수 이론을 체계적으로 배우기 보다는 함수형 프로그래밍에 근간이 되는 람다 대수가 어떤 느낌인지 확인하는 정도이기 때문에 여기에서 마무리해도 충분해 보인다.



Top comments (0)