Breve introducción a Algoritmos Genéticos

(el contenido también se encuentra disponible en formato de IPython notebook)

¿Qué es un algoritmo genético?

Un algoritmo genético es un método para resolver un problema inspirado en el proceso de selección natural propuesto por Charles Darwin:

As many more individuals of each species are born than can possibly survive; and as, consequently, there is a frequently recurring struggle for existence, it follows that any being, if it vary however slightly in any manner profitable to itself, under the complex and sometimes varying conditions of life, will have a better chance of surviving, and thus be naturally selected. From the strong principle of inheritance, any selected variety will tend to propagate its new and modified form

Hay muchas variaciones de dichos algoritmos pero todos siguen a grandes rasgos este patrón:

1. Generar una población de individuos (o cromosomas en el léxico de los algoritmos genéticos)

2. Evaluar a los individuos de la población por una métrica de aptitud (conocido como fitness)

3. Sólo quedarse con los N sujetos de la población más aptos

4. Crear una nueva generación de individuos a partir de los más aptos a través de:

   1. cross breeding: "cruza" entre individuos
   2. mutations: mutaciones aleatorias

5. Volver a paso 2 y repetir

¿Qué problemas se pueden resolver?

Los problemas atacados por estos algoritmos son en general de optimización de funciones (más adelante veremos como esto se puede generalizar a soluciones más interesantes), por ejemplo, dada una función:

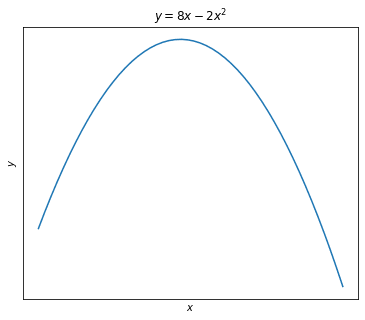
y = 8x - 2x^2

def f(x): return 8 * x - 2 * x**2 

Nos interesaría encontrar el punto máximo, es decir el valor de x que maximiza y.

Vamos a usar un algoritmo genético para esto, apoyándonos en la librería evol de python

Paso 1: Primera Generación

Para comenzar tenemos que armar una primera generación de individuos o cromosomas, en este caso los individuos serían distintos valores de x.

Imaginemos que no sabemos dónde está el máximo de la función pero tenemos una vaga idea de en qué rango puede estar. Para este ejemplo vamos a suponer que el valor está entre -1.000.000 (menos un millón) y 1.000.000 (un millón).

Nuestra primera generación tomará valores aleatorios en este intervalo:

np.random.seed(1234) # make results reproducible.


def random_guy(): return np.random.randint(low=-1_000_000, high=1_000_000)


initial_generation_size = 100
first_generation = [random_guy() for _ in range(initial_generation_size)]

Con esto podemos crear nuestro objeto Population. También le pasamos la función a optimizar ($f(x)$ definida más arriba) y le aclaramos a evol si la idea es maximizar o minimizar dicha función:

pop = Population(chromosomes=first_generation, eval_function=f, maximize=True)

Supervivencia del más apto

De nuestra población inicial queremos quedarnos sólo con el 10% que mejor performó, los más aptos. Para esto tenemos la función survive:

survivors = pop.survive(fraction=0.1)

CrosBreeding y Mutaciones

Con los sobrevivientes vamos a crear una nueva generación, producto de breeding y mutaciones aleatorias.

Para esto tenemos que definir tres funciones:

1) una para elegir dos padres del conjunto de supervivientes (lo haremos al azar)

2) otra para definir cómo dos individuos de la población crean un nuevo individuo 😏

3) una última para determinar las mutaciones aleatorias

Entonces:

def pick_parents(population):
    mom, dad = np.random.choice(population, size=2)
    return mom, dad


# the child is the mean between two parents.
def make_child(mom, dad):
    return (mom + dad) / 2


# add gaussian noise with mean zero.
def random_noise(individual, sigma):
    noise = np.random.normal(loc=0, scale=10) * sigma
    return individual + noise


new_generation = survivors.breed(parent_picker=pick_parents, combiner=make_child).mutate(random_noise, sigma=1)

It's evolution, baby

Con la nueva generación podemos repetir el proceso indefinidamente (seleccionar, cruzar, mutar).

Vamos a hacerlo unas cuantas veces y nos quedamos con el individuo más apto de cada generación:

def fittest(generation):
    fit = sorted(generation.evaluate(), key=lambda x: x.fitness)[-1]
    return fit.chromosome


generations = 120
fittest_of_each_gen = []

gen = new_generation
for _ in range(generations):
    survivors = gen.survive(fraction=0.1)
    new_gen = survivors.breed(parent_picker=pick_parents, combiner=make_child).mutate(random_noise, sigma=1)
    fittest_of_each_gen.append(fittest(new_gen))
    gen = new_gen

Analizando los resultados

Volvamos otra vez a la función original y sobre la línea agreguemos los "mejores exponentes" de cada generación.

Las generaciones van de menor a mayor desde el azul (cool) al rojo (warm). También graficamos el error, o sea qué tan alejados estamos del valor máximo real, en función del número de generación:

Como vemos aproximadamente en la generación 100 el valor empieza a converger con el máximo real.

Conclusión

Pero, ¿Tiene sentido utilizar está técnica? después de todo, sabemos que la forma de encontrar el mínimo de una función como

f(x) = 8x - 2x^2

es tomar su derivada

f'(x) = 8 - 4x

y encontrar el valor donde el gradiente es cero, en este caso

f'(x) = 8 - 4 * 2 = 0

La respuesta es que, si bien para este caso es un overkill, los algoritmos genéticos son un método numérico que nos permite encontrar resultados aceptables en funciones no diferenciables o de las que no se conoce un método análitico.

Próximamente

Con esto concluimos esta breve introducción.

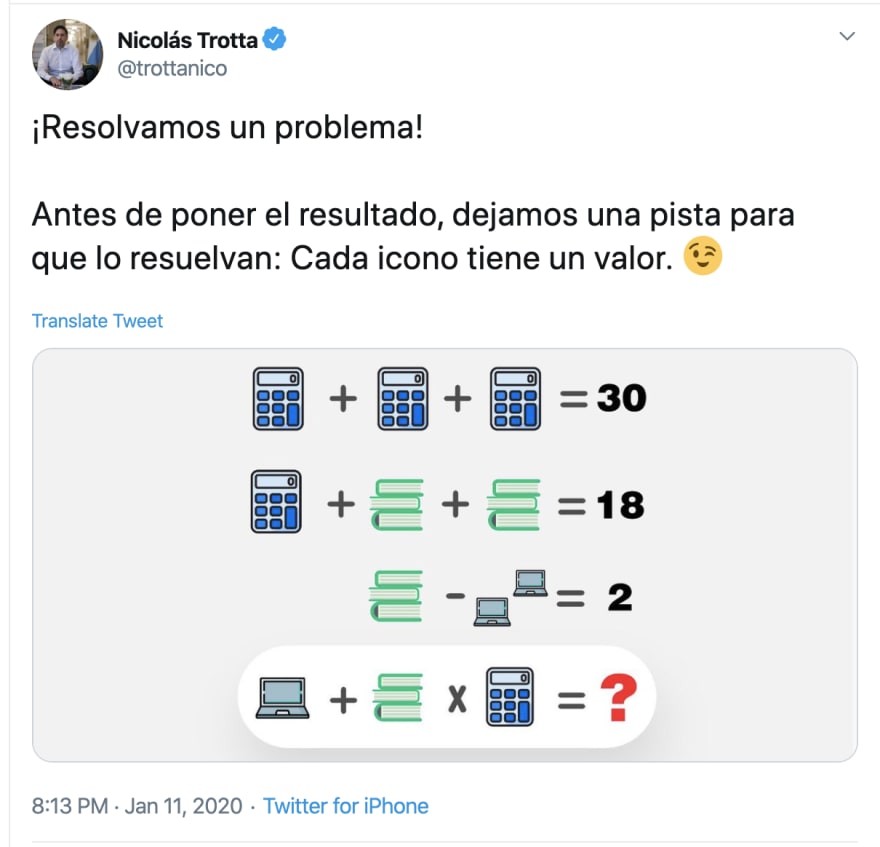
En un próximo post, analizaremos como performa este mismo algoritmo genético para resolver el conjunto de ecuaciones que presentó el ministro de educación hace unas semanas: