Hello! My name is Jay Steigner and I am a student software developer currently attending Operation Spark in New Orleans. This is my first blog so here goes! Have you ever heard of a B-Tree and wondered what the heck is that? Well you are in for a treat! In this blog I'll be covering what is a B-Tree, the rules that govern their self balancing, and why we use them. Lets dive in!
In order to know what a B-Tree is I must first give a little background into what a 'tree' in computer science means. A 'tree' is an organizational structure for the storage and quick retrieval of data. We refer to each individual container of data as a node. In computer science, when we think of a 'tree' we visualize an upside down 'tree' with the root node being at the top and the leaf nodes being at the bottom with children nodes in between.
The B-Tree data structure was invented by Rudolf Bayer and Ed McCreight while working at Boeing Research Labs in 1972. If you have ever heard of a Binary Search Tree then after reading this blog you will realize that the B-Tree and Binary Search Tree both employ similar concepts. I like to think of the B-Tree as the Arnold Schwarzenegger of Binary Search Trees because they are designed to hold massive amounts of data.
So what is a B-Tree? A B-tree is a self-balancing tree data structure that maintains sorted data and allows for searches, sequential access, insertions, and deletions in logarithmic time. They are an excellent data structure for storing huge amounts of data for fast retrieval.
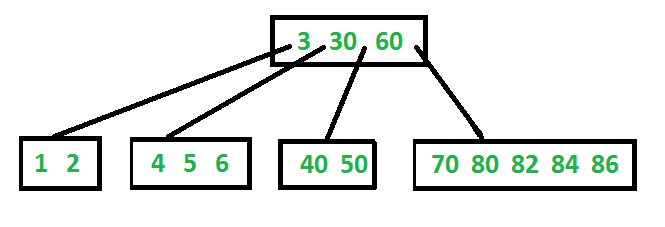
Here is an example of what a small B-Tree would look like. One important aspect of the nodes of a B-Tree is that they can hold multiple values. Here we have our root node which has three values or keys in it and it has four leaf nodes. This is not a coincidence but is done by design and these concepts are relative to each other.
The basic concept behind a B- tree is that all the values in the far left node will be less than the first value in the root node, all the values in the adjacent right node will be between the first and second values found in the root node, all the values in the next node will be between the second and third values in the root node, and finally all the values found in the far right node will be greater than the last value in the root node. So you can think of the values found in the root node the same way you would think about an index in an encyclopedia.
The rules that govern how a B-Tree will self balance itself are known by the parameter given to it in the name. So in this example, this is called a B-Tree of Order 5 because it can have up to 4 values in a specific node and and a max of five children before it will have to self balance. If you try to insert data into a leaf node that is already full, the node will split into two with the smaller half going into a new left node and the larger half going into a new right node and the median value will be promoted to the parent node.
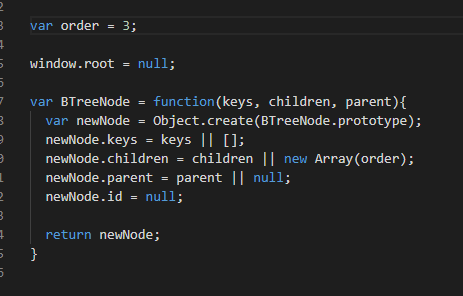
Here is an example of what the code to make a new node would look like:
But there are more rules that determine the self balancing. Every node will have at most M children. A non-leaf node with X children can contain at most x - 1 values. So a non-leaf node with 3 children will have at most 2 values. Every non-leaf node except the root has at least the result of the ceiling of m/2 children. The ceiling just means rounding up after dividing m/2 and the value of M is supplied with the name of the B-Tree. So for our order 5 B-tree, if we divide 5/2 which is 2.5 and round up to three then every non-leaf node will have at least 3 children. Another important aspect of B-Trees is that all bottom leaf nodes appear in the same level. All of these rules are what make it self balance so efficiently and help it maintain that precious logarithmic time complexity which is crucial when trying to access data stored in a huge database.
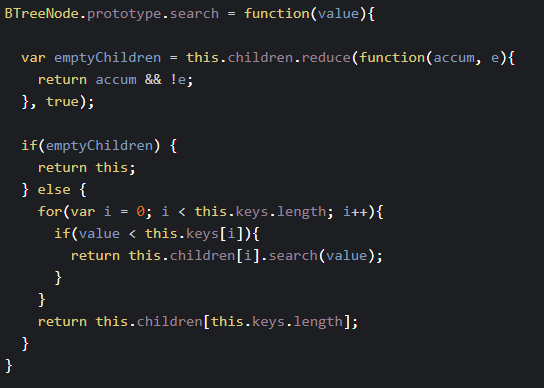
Here is an example of what the code for a search method on a B-Tree would look like:
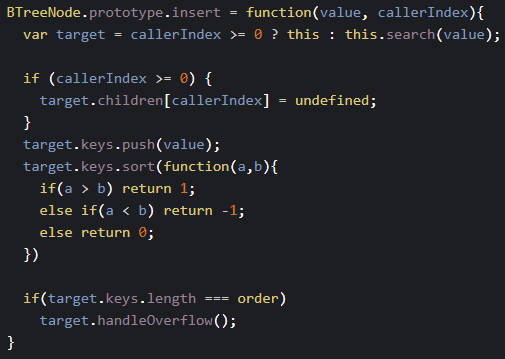
Here is an example of what the code for an insert method would look like:
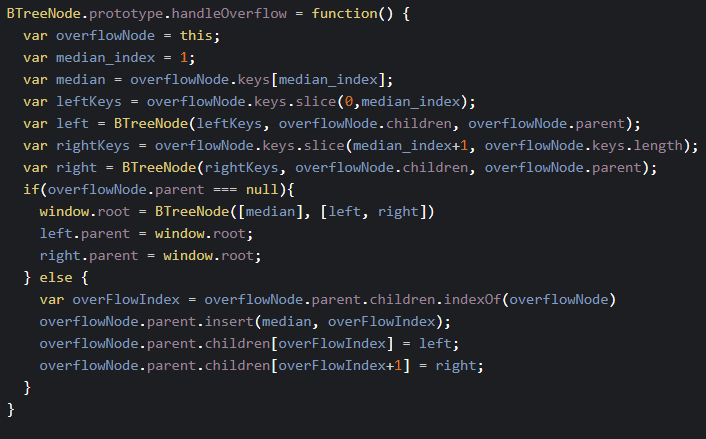
And last here is an example of what the code to deal with resizing would look like:
So in conclusion the reason we use the B-tree is because of its optimal self-balancing nature which retains logarithmic time complexity and makes it well suited for storage systems that read and write relatively large blocks of data, such as discs. Therefore it is commonly used in databases and file systems. So if you have to create a big database I highly recommend using the B-Tree.



Top comments (0)