3D Computer Graphics
Computer graphics is an art of drawing pictures on computer screens with the help of programming. It involves computations, creation, and manipulation of data. In other words, we can say that computer graphics is a rendering tool for the generation and manipulation of images.
In the 2D system, we use only two coordinates X and Y but in 3D, an extra coordinate Z is added. 3D graphics techniques and their application are fundamental to the entertainment, games, and computer-aided design industries. It is a continuing area of research in scientific visualization.
Furthermore, 3D graphics components are now a part of almost every personal computer and, although traditionally intended for graphics-intensive software such as games, they are increasingly being used by other applications.
Contents
- Projection 투상변환
- Translation & Rotation
- Polygon Meshes
- Morphing
- Projects
Projection
가시변환 Viewing Transformation이라고도 불리는 투상변환은 3D 물체를 2D 화면으로 매핑하는 작업을 말한다.
- View Plane, Projection Plane : 투상면
- View Point = Eye Position = Camera Position = COP : 관찰자 위치
- Projectors : 물체 곳곳을 향한 투상선
- Line of Sight : WCS 원점 또는 초점을 향하는 시선
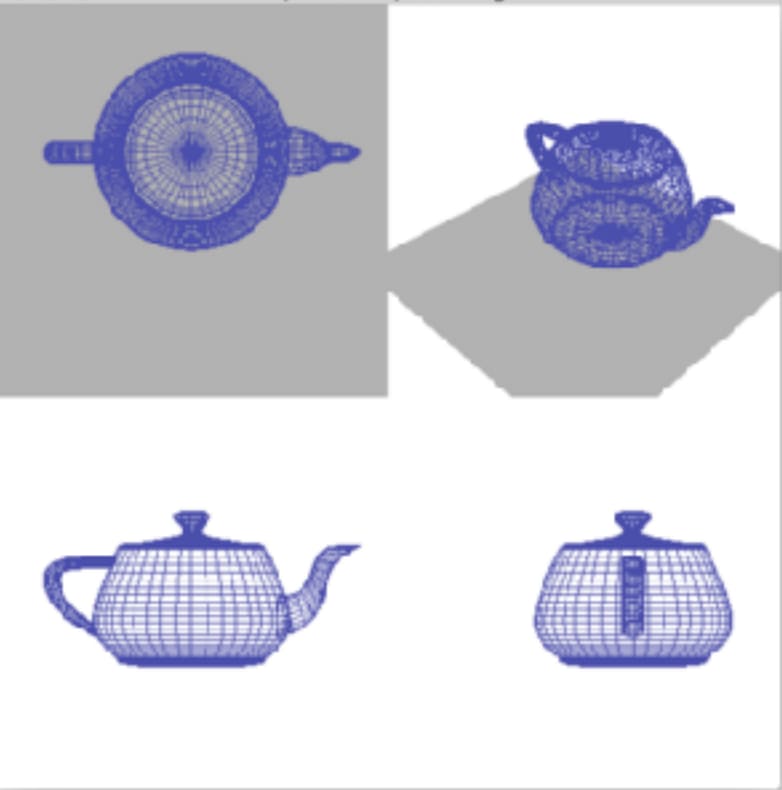
Parallel Projection
평행투상 - 시점이 물체로부터 무한대의 거리에 있다고 간주
- 투상선이 평행
- 물체의 평행선은 투상 후에도 평행
- 시점과의 거리에 무관하게 같은 길이의 물체는 같은 길이로 투상
Parallel projection discards z-coordinate and parallel lines from each vertex on the object are extended until they intersect the view plane. In parallel projection, we specify a direction of projection instead of center of projection. In parallel projection, the distance from the center of projection to project plane is infinite. In this type of projection, we connect the projected vertices by line segments which correspond to connections on the original object.
Perspective Projection
원근투상 - 시점이 물체로부터 유한한 거리에 있다고 간주
- 투상선이 방사선 모양으로 퍼짐
- 카메라나 사람의 눈이 물체를 보는 방법
동일한 크기의 물체라도 시점으로부터 멀리 있는 것은 작게 보이고 가까운 것은 크게 보임
소실점 (VP : Vanishing Point) 원근투상 결과 평행선이 만나는 점 = 시점 높이
소실점의 개수에 따라 일점투상, 이점투상, 삼점투상
-
원근변환을 사용할 경우 물체 정점간의 거리에 대한 축소율이 달라짐
- One point perspective projection is simple to draw.
- Two point perspective projection gives better impression of depth.
- Three point perspective projection is most difficult to draw.
Translation & Rotation
Translation
In 3D translation, we transfer the Z coordinate along with the X and Y coordinates. The process for translation in 3D is similar to 2D translation. A translation moves an object into a different position on the screen.
Rotation
3D rotation is not same as 2D rotation. In 3D rotation, we have to specify the angle of rotation along with the axis of rotation. We can perform 3D rotation about X, Y, and Z axes.
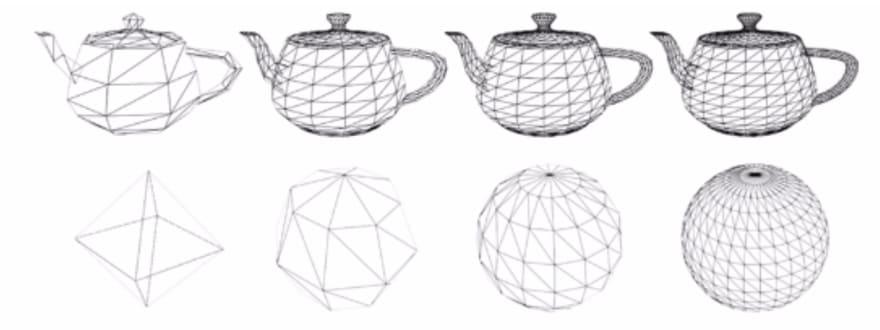
Polygon Meshes for Rendering
렌더링 전 물체의 표현을 만드는 작업을 모델링이라고 부르는데 ,
음함수로는 GPU를 표현하기 어려운 점이 있어 평면의 개수를 샘플링 하는 과정을 거친다. 이때 일정한 꼭지점이 샘플링 되는데 그 꼭지점들을 선으로 이어 다각형으로 만든다. 이를 폴리곤 메시라 부르며 좌표도 3차원으로 표현이 되고 vertex array 셀에는 좌표 이외에도 많은 정보들이 저장된다.
3D surfaces and solids can be approximated by a set of polygonal and line elements. Such surfaces are called polygonal meshes. In polygon mesh, each edge is shared by at most two polygons. The set of polygons or faces, together form the “skin” of the object.
This method can be used to represent a broad class of solids/surfaces in graphics. A polygonal mesh can be rendered using hidden surface removal algorithms. The polygon mesh can be represented by three ways
- Explicit representation
- Pointers to a vertex list
- Pointers to an edge list
Advantage
- It can be used to model almost any object.
- They are easy to represent as a collection of vertices.
- They are easy to transform.
- They are easy to draw on computer screen.
Disadvantages
- Curved surfaces can only be approximately described.
- It is difficult to simulate some type of objects like hair or liquid.
Morphing
하나의 물체가 전혀 다른 물체로 변화하는 기법. 두 개의 서로 다른 이미지나 3차원 모델 사이의 변화하는 과정을 서서히 나타낸다. A -> B
A

B

Morphing is an interpolation technique used to create from two objects a series of intermediate objects that change continuously to make a smooth transition from the source to the target. Morphing has been done in two dimensions by varying the values of the pixels of one image to make a different image, or in three dimensions by varying the values of three-dimensional pixels. We're presenting here a new type of morphing, which transforms the geometry of three dimensional models, creating intermediate objects which are all clearly defined three-dimensional objects, which can be translated, rotated, scaled, zoomed-into.
Conclusion
ComputerGraphics you can overview computer graphic projects in my github.


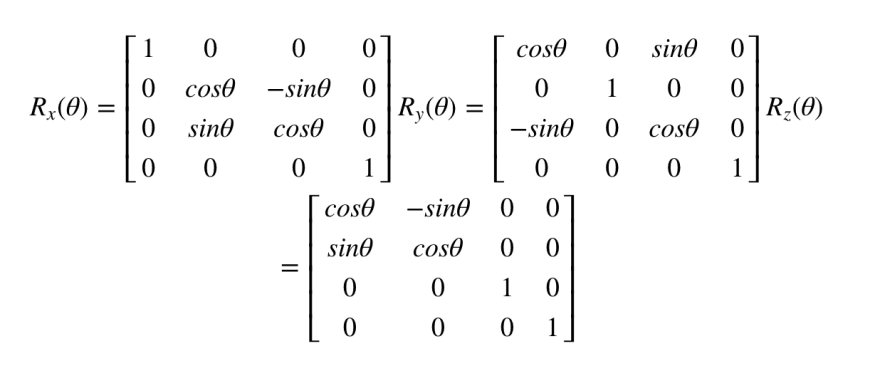

Top comments (0)