This has been originally posted on my personal blog.
Dear programmer! I think it's time we talk about regular expressions. What do you think?
Yes, I understand you know them and can use in most common real-life situations. It's great! I know some programmers, for whom more complicated regular expressions are quite a black magic. Even though they may have quite a few years of experience. But I don't want to preach you about how to build a regexp1 to get your problem solved. I intend to explain how they work internally and what consequences it might have for us.
So, where do we start? It actually begins with mathematics. In particular, with one mathematical construct called a finite automaton. Even though its formal definition might sound scary, it is a pretty simple idea. And it's easy to visualize, so don't worry.
A finite automaton is a set of states (commonly named q1, q2, q3 etc.), connected by transitions. The latter are like edges in a directed graph: they are one-way (therefore visualized with arrows) and also have a label assigned to them. One (and only one) of the states is marked as initial or starting (usually also named as q0) and at least one is final or accepting state.
We say that automaton is build over an alphabet, which is a set of characters allowed in transition labels. We also have an input which is simply an array of characters on which automaton is run. What does it mean?
We start at the initial state. We take the first character from input and find a transition which is labeled by that character. We follow the transition, changing our current state to the one on the end of it (this might be the same state). Then we take another character and do the same. Repeat, until the end of the input. (Did I mention it has to have finite length? Well, it has to.)
The result might be on of the following:
- We end up in one of the accepting states. Good. This means that the automaton accepted the input.
- We end up in some non-accepting state. This means that input was not accepted by our automaton.
- At some point we did not find and transition labeled by currently processed character. This in not an exception – just means that the input was not accepted too. Obviously, if input contains any characters not from the alphabet the automaton was built on, it won't be accepted.
With regular expressions, we take their definition (for example /abc/), then build an automaton and run a string through it.
Examples
Let's see some finite automata for some regular expressions.
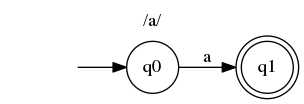
In this very simple example, we start in q0 state. If our input is "a", we can transit via the only transition to q1. The input is consumed, we are in an accepting state (denoted by double circle), so the string matches the regexp.
Note that for string "aa" after consuming first character we still have one a to go. But there is not transition outgoing from q1, so we cannot accept the string. This might be counterintuitive to what you know from programming, but in reality /a/ regular expression is actually /\Aa\z/. We are going to treat them this way in the rest of the post.
Meanwhile, let's have a look at some more examples.
Epsilon transitions
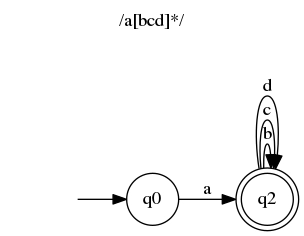
The last example is a bit more complex and introduces something we did not talk about yet: epsilon transitions. This is a convenience mechanism to have your graphs/automata simpler and easier to reason about. What are they?
Epsilon transition is done without consuming any character from input. So, if we are in q1, we can go to q2 "for free".
Sounds stupid? Well, it does for me. It means that after consuming a in last example (/a[bcd]*/) we are both in state q1 and q22. Fortunately, there is a simple algorithm to get rid of epsilon transitions. It creates automaton that is more "precise" but is less pretty and harder to read. It is also usually easier to build some automata from regular expressions using epsilon transitions.
Here is equivalent automaton without epsilon transitions:
I won't go into details about the algorithm, but the main idea is:
For each transition, when it leads to state, from which epsilon transition originates, replace it with a transition to target state of the epsilon transition. Then remove epsilon transition. Repeat until no epsilon transitions are left. Then prune states which are orphaned (no transitions in or out).
Sometimes it is a bit harder than that, but we are not going to use a lot of epsilon transitions here, so we don't need to concentrate on that.
Deterministic or not?
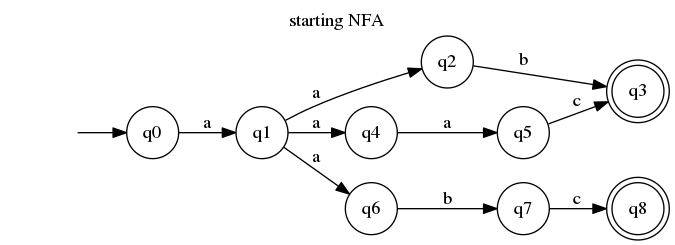
So far our automata were fairly simple. You probably already thought once or twice about how to implement them. However, we did not cover one really important part of regular expressions - alternation. Consider a regular expression: /ab(cd|ce)*/. Now, of course this could be written in smarter way (/ab(c[de])*/) but it's not like we have much choice. The regular expression is valid so we have to create an automaton for it:
The problem arises when we are in state q2 and have c on the input. Should we go to q3 or q5? As humans, we can look ahead and see it clearly, however this luxury is not available for automata. We always need to change state in the very moment of consuming a character. So in the implementation we'd need to be in many states simultaneously. While this is not so bad, actually, it can be a bit slow for larger automata. Can we do better?
To name a problem: our automaton is non-deterministic. A definition for it is that it's not a deterministic automaton (.___.). So what is the latter? From Wikipedia:
- each of its transitions is uniquely determined by its source state and input symbol, and
- reading an input symbol is required for each state transition
So, we can't have epsilon transitions and for each state, only one transition with a given label can originate from. Simple. Let's do this.
Determinization of NFA
For purpose of explanation, I going to determinize the following automaton:
As you might instantly notice, the problem appears when we are in q1 state and have a character a in the input. Which state are we transitioning into? Well, according to informal definition of non-deterministic automaton, we are in three states at once: q2, q4 and q6.
The determinization process takes advantage of that definition and makes it apparent by creating a new state denoting that. For convenience, we'll call it q2,q4,q6. We create a transition from q1 to our new state via a and delete all the other a-labeled transitions originating from q1 This is how our automaton look after this first step:
As you see, it's a bit broken right now. We need to take care of the detached parts, starting with q2, q6 and q4. That's where our naming convention comes to help. Starting with q2, we are going to take all its transitions and attach them to all "set states" which include q2 (in this case it's our new big state). We create transition to q3 via b.
Then we do it with the rest of detached states. From q4 we can go to q5 via b, so now we create a transition from q2,q4,q6 to q5 via b. And for the q6 – via b we can reach q7 but we already have a transition labeled by b (to q3). To resolve this conflict, instead of q3 we create another "set state" q3,q7.
Another important thing: q3 was an accepting state. Our newly created q3,q7 state should be accepting too. This also comes from informal NFA definition: if we are in multiple states but at least on of them is accepting, the automaton accepts the input consumed so far.
Only one detached state is left and we have to repeat what we have done in previous step: take it, find all "set states" that include q7 (in this case only q3,q7) and rewrite the transition.
We can now enjoy a deterministic equivalent of our initial non-deterministic automaton. It became a bit simpler (7 states instead of 9 and 6 transitions instead of nine). By reverse engineering it into regular expression, we also have a simpler one! The regexp for NFA is /a(ab|aac|abc)/ and for our DFA is /aa(bc?|ac)/.
This is not always that obvious though and sometimes deterministic automata are more complected that their non-deterministic counterparts.
Complete automata
If you know automata theory and especially if you are a mathematician, you might be fuming right now and almost scrolling to comments to tell me that the above is not a deterministic finite automaton. You are right, actually. I left out one thing but you will soon understand why.
A formal definition of deterministic automaton requires it to be complete. What does it mean? That for each state and each character of the alphabet, there should be a transition originating from the state and labeled by the character. Which means we need to have a lot of transition, but as a bonus we will never end up in a situation where we have not consumed the whole input, but we cannot continue because of no matching transition.
This is achieved by introducing one extra state. We used to call it "hell". With it, and assuming our alphabet is simply {a,b,c,d}, we can make our DFA complete. Like this:
So, now it's not readable, even though I drew it in concise way. However, with regular expressions in programming, we usually want our alphabet to consist of all unicode characters. And there's a lot of them. I mean, a lot. That's why we usually do not want to create complete automata.
And here we are
This is basically it for now. A deterministic automaton is a result of regexp compilation. Now we can throw some string into it and it will accept them or not. I planned to put an example implementation too, but the post is lengthy already, so I'll schedule it for part 2. Some final notes about what we did so far:
- We now know how to construct automata for regexp consisting of some basic features, such as
*,+,(),|. I did not cover it, but it's also possible to have{n},{n,},{n,m}and also?. - We don't know how to handle ranges and groups. Also, how to proceed with a dot (matching any character). These are really implementation details that do not matter from theoretical point of view. Especially dot requires some tricks when we want it to match any unicode character, but we won't talk about it now.
- We cannot use backreference, lookahead or similar features. Even stronger, we won't be able to use them, because it is impossible to create finite automaton to handle them. You need different theoretical device (automaton with stack, I think), but that's a whole different story...
- All examples presented above are in fact
/\Aabc\z/, not just/abc/. You would have to create a set of all substrings to run against the automaton and check if any of it matches. This is not convenient but also it is why you should use\Aand\zwhenever possible, because it will be faster. - Creating an automaton and later determinization of it is costly, comparing to just running it against an input. If you are not sure that your language will internally optimize it, you should always compile a regexp outside of any loops. It is instant and free optimization. Now you know why.
- As an addition – if you are writing some performance-critical code, you should always consider using something else than regexp in the first place. Checking if one string is a substring of the other is much faster than checking that with regular expression. So no more
if user_agent =~ /Explorer/from now on, okay?












Top comments (6)
This is a fantastic article, always struggled to get my head around how this stuff works but you explained it really clearly! Reminds me of Andrew Gallant's blog post about how he used finite state machines to index text really (really, really) fast - worth a read if this kind of stuff is your jam :)
Hey great post, I was wondering, what tool did you use to create those diagrams!
Thank you! Diagrams were created using Graphviz. Here I put some examples (the first and the last diagram from post): gist.github.com/katafrakt/d9458d61...
Great post! Looking forward to the 2nd part!
great article, i studied this back at the university i think it was called language theory
Very good post. thank you for writing it.