“Merge sort” is popular algorithm for sorting an array from smallest to largest. It is often compared to selection sort, insertion sort, bubble sort and many others.
However, as I searched the internet for a simple explanation of how merge sort works… I could not find a guide that made it incredibly simple.
Sure, there is a beautiful visualization over at VisuAlgo, and FreeCodeCamp has a comprehensive text explanation.
But, I still found myself staring at code blocks for a long time and wondering, “What exactly is happening in this line?”
So, this guide will give an incredibly simple explanation of how merge sort actually works. It is kind of like a series of tennis tournaments.
In order to understand this guide, you just need to know the basics of recursion. Let’s get started!
The Basics of Merge Sort
One of the fundamental ideas of merge sort, like all other basic JavaScript algorithms, is that you can only sort an array by comparing two elements at a time and finding the larger element.
So, we need a way to run those comparisons as efficiently as possible.
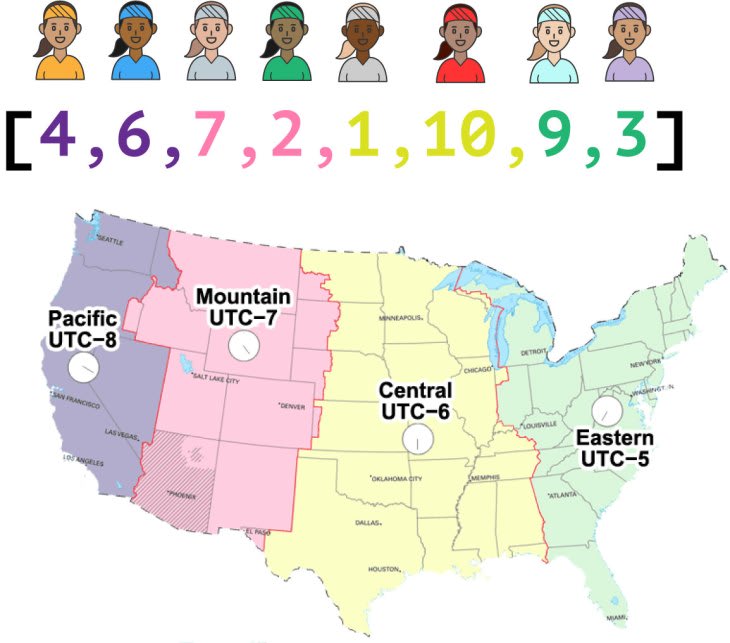
Let’s imagine that we have an array of 8 numbers that we need to sort from smallest to largest:
[4,6,7,2,1,10,9,3]
Rather than thinking of these as numbers, let’s think of them as skill levels of tennis players, on a scale of 1-10. It’s our job to determine, “Who is the best tennis player of the group?”
So, using merge sort, we need to rank this group from lowest skill to highest skill. We can do that by running a series of tennis matches and determining the winner of each one.
But, in real tennis competitions, players are not forced to travel across the country to compete in one massive tournament. Instead, they must win a series of smaller tournaments before they can compete for the prize of national champion.
Let’s imagine that we are trying to find the best amateur player in the United States.
We can group these players into 4 regions: West, Mountain, Central, and East. It would look like this:
The elements at index 0 and 1 in the array in purple are in the West region… you get the idea.
We will start with 4 regional tournaments, and then run competitions between regional winners to determine a national champion.
In other words, we will consistently find the “better” of two tennis players until we reach the national level. At the national level, the “better” player is really the “best” in the United States!
Setting Up The Merge Sort Algorithm
Okay, I admittedly chose 8 players because it is easy to show within a blog post. In order for the algorithm to work properly, it must be able to handle all arrays with at least 2 elements.
And, it needs to handle cases where there is an odd number of elements in the array ie 9 elements.
There are really two parts of merge sort:
- Dividing the array of all tennis players into regional tournaments
- Running the tennis matches at a successively higher level until we are able to determine a national champion.
Here’s why we need recursion: we have no idea how many matches need to be run until we know the size of the array. This algorithm must be able to handle 8 tennis players… or 350.
We will cover the recursion part later. Now, let’s focus on part 2, the “competition” function that allows us to compare two tennis players and resort them based on their skill level. We will assume the better player wins every time.
This function can be run an infinite number of times, depending on the size of the player pool.
This function should take two arrays, and combine them into one properly sorted array, from smallest to largest. It should do this via “competitions”, or 1 on 1 comparisons.
Here’s what this looks like for two arrays with two elements apiece. This might be the tournament that happens AFTER the regional tournaments have happened.
Here’s a couple key notes about the GIF above:
- We can only move one player at a time. This is because we only know if one player is better than the one we are facing. We can’t determine the absolute position of multiple players at once.
- One side of the tournament could have all the best players. Therefore, we need to be able to handle the case where only one side of the array has players remaining.
Here’s what the code looks like:
const tournament = (left, right) => {
var rankings = [];
while(left.length || right.length) {
if(left.length && right.length) {
if(left[0] < right[0]) {
rankings.push(left.shift())
} else {
rankings.push(right.shift())
}
} else if(left.length) {
rankings.push(left.shift())
} else {
rankings.push(right.shift())
}
}
return rankings;
}
That’s a lot at once. Here’s a summary:
- Line 3: We start iterating through the players on both sides of the bracket. The number of iterations is determined by the longer array.
- Lines 4-10: We “compete” with the first element in each array. When we find a loser, we use the shift() method to remove the player from the tournament and add it to the next lowest spot in the rankings array.
- Last Line: We return the rankings array with the players ranked from worst to best.
Here’s an animated version of that code:
Okay, now let’s move back to the first function to see how we split the players up into tournaments at the regional level and then combine them back into a national tournament.
Using Recursion Within Merge Sort
Okay, we now have the function that allows us to run “competitions”, but we need a function to split up the array and put it back together.
Before we can run any competitions, we need to organize the array into “regions” before we can run the first 1v1 competition.
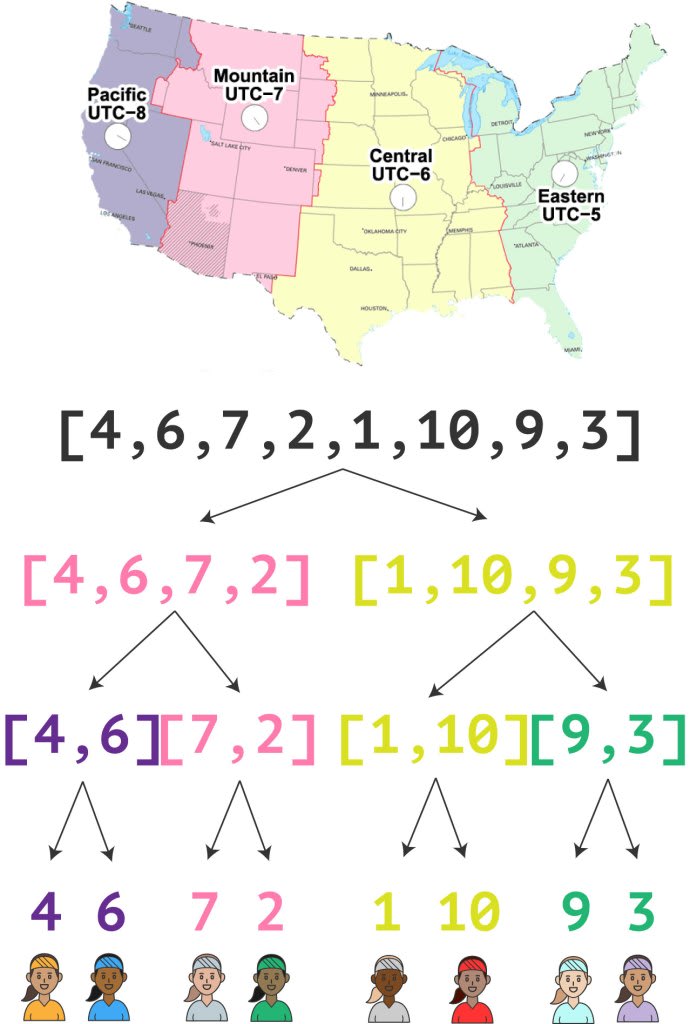
Here’s how we might go from 8 players of various skill levels to four 1v1 competitions:
There are 7 examples of an array being split into a smaller array or a single element. We cannot hardcode this number because if there were 16 players, there would be 15 examples of an array being split.
Remember: in 1v1 comparisons, we can only tell which player is “better” than another. That’s why we need to break this down into 1v1 comparisons- so that all the smaller arrays are properly sorted before they are compared later.
And, afterwards, we will reassemble the array after sorting the elements at every layer.
Here's how the array will be split up into a series of 1v1 competitions:
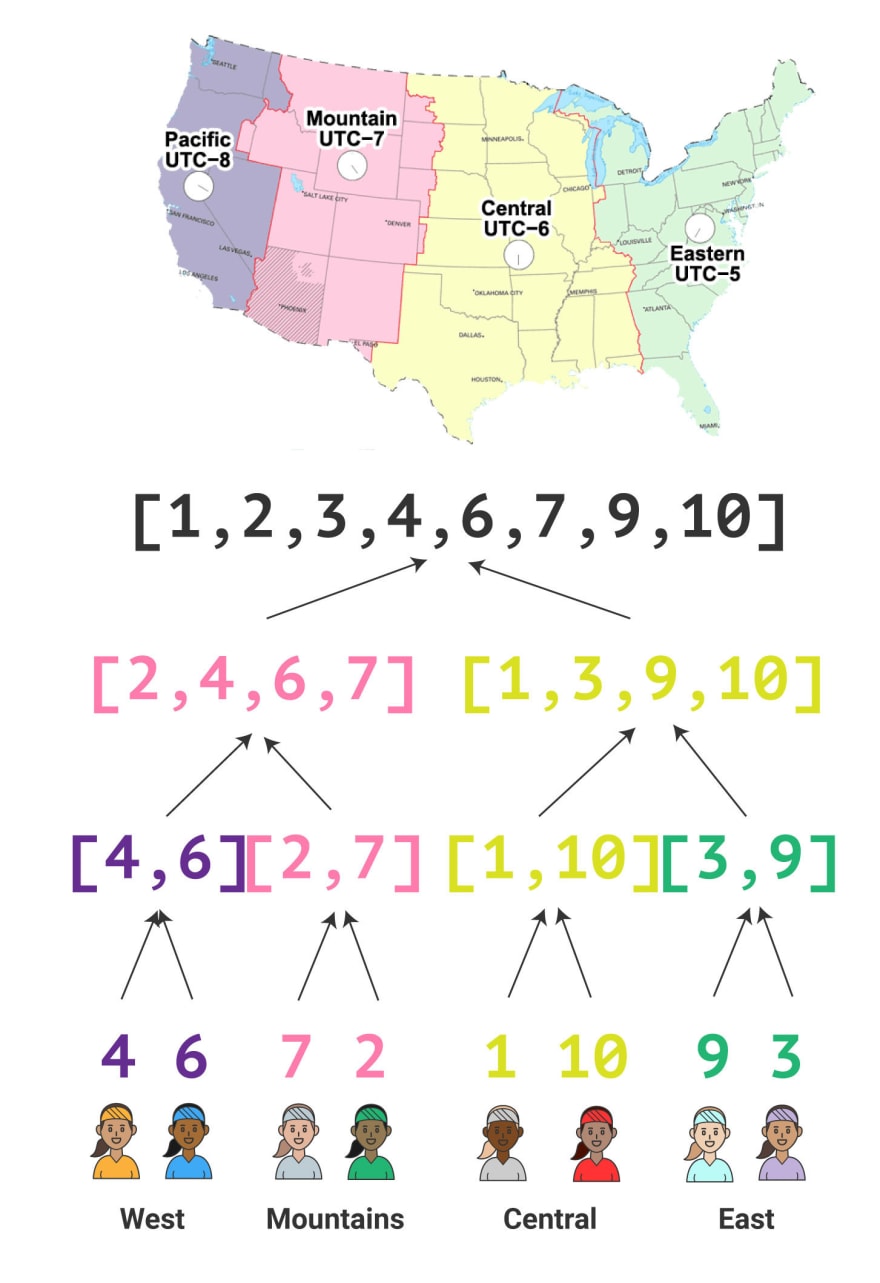
And here's how we will "reassemble" the array to find the ranking from smallest to largest:
See the parallels between the array splitting and then reassembling? This is a great hint that we will need recursion.
I will focus in on the “left” side of the array, or the first half. Here’s how we can build a call stack that will allow us to sort the array.
Every time we split the array in half, we add a call to the call stack that references the previous call. At the end, we can run the tournament() function at each level to sort each smaller array before mergining them.
Here’s what the code looks like:
const findWinner = (players) => {
if(players.length <= 1) return players;
const middle = players.length / 2 ;
const left = players.slice(0, middle);
const right = players.slice(middle, players.length);
return tournament(findWinner(left), findWinner(right));
}
let players = [4,6,7,2,1,10,9,3];
findWinner(players);
Lines 3-5 allow us to define a midpoint in the array, and split the array down the midpoint. When we do this recursively, we shrink the array until it is a single element.
The most important code is in lines 2 and 6.
In line 2, we handle the case where the array has been shrunken to 1 element. This tells us that the recursion should stop, and we can run the lowest-level, regional tournament.
In line 6, we define that in each call, we will run the tournament() function on the sorted array from the previous call (or a 1v1 matchup, if it is the lowest level)
Here’s what this looks like:
In the example above, we have gotten to the level of 1v1 in the “West” and “Mountain” region. So, we can start at the top of the call stack and find the top player by the time we get to the end of the call stack using the tournament() function multiple times.
Get The Latest Tutorials
Did you enjoy this guide? Get my latest visual explanations of HTML, CSS and JavaScript topics on the CodeAnalogies blog.









Top comments (5)
Hello Kevin,
You return the wrong variable in the tournament function in your code example. Instead of returning
resultyou should returnrankings.Other than that it is a great reat post on how merge sort works and how you implemented it!
Keep up the good work!
Hey, did you mean to post this on my "merge sort" article? I will take a look!
Hello,
It's meant for this article on the "Setting Up The Merge Sort Algorithm" section.
Good point, fixed
Talking about tennis, it’s amazing how the sport combines physical skill with mental strategy. I’ve been following some of the major tournaments recently and diving into the details of player stats and match outcomes. It's fascinating how much detail and analysis goes into predicting match results. This reminds me of how complex recursion can be in programming, where each call depends on the previous one ggbet.win/en/tennis Both require a deep understanding to fully appreciate their intricacies. Does anyone have a favorite player or match that really stood out to them recently?