Breadth-First Search (BFS) Algorithm

Let's Imagine This first,
You’re in a maze of rooms. You want to find the shortest way out. So you start from the first room, check all the adjacent rooms, then go to the next layer of rooms, and keep expanding until you reach the exit.

That’s Breadth-First Search (BFS) – you explore layer by layer, level by level.

What is BFS?
Breadth-First Search (BFS) is one of the most fundamental graph traversal algorithms. Instead of diving deep into a single path, BFS explores nodes level by level, ensuring that all neighbors of a node are visited before moving deeper.

It’s especially powerful when you need to find the shortest path in an unweighted graph

How It Works
1.Start from a source node

• Choose a node to begin with (for example, node 0).
• This node will be the root of your traversal.

2.Use a queue (FIFO) to track nodes to visit next

• A queue is the ideal data structure because BFS needs to process nodes in the same order they are discovered.
• First In → First Out ensures that we finish exploring one "level" of neighbors before moving on to the next.

3.Keep a visited[] array (or set)

• To avoid infinite loops (e.g., in cyclic graphs), we maintain a record of which nodes we have already visited.
• This ensures we never process the same node twice.

4.Process nodes one by one

• Take the front node from the queue.
• Look at all of its neighbors:
  • If a neighbor has not been visited → mark it visited and add it to the queue.
• Continue this until the queue becomes empty.

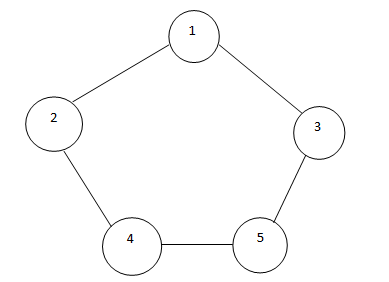
Let's understand With Dry Run of Simple Example (Graph)

Step 1
Visited Node: 1

We start with node 1, mark it visited, and add its neighbors (2 and 3) to the queue.

Step 2
Visited Node: 2 (front of queue is dequeued)

From node 2, we explore its neighbors. Node 4 is unvisited, so it is added to the queue.

Step 3
Visited Node: 3

From node 3, we explore neighbors. Node 5 is unvisited, so it gets added to the queue.

Step 4
Visited Node: 4

Node 4 has neighbors (2 and 5). Both are already visited/queued, so nothing new is added.

Step 5
Visited Node: 5

Node 5 has neighbors (3 and 4). Both are already visited, so BFS traversal is complete.

✅ Traversal Order: 1 → 2 → 3 → 4 → 5

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

vector<int> bfsOfGraph(int V, vector<int> adj[]) {
    vector<int> bfs;
    vector<bool> visited(V, false);
    queue<int> q;

    // Start BFS from node 0
    q.push(0);
    visited[0] = true;

    while (!q.empty()) {
        int node = q.front();
        q.pop();
        bfs.push_back(node);

        for (int neighbor : adj[node]) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }

    return bfs;
}

int main() {
    int V = 5;
    vector<int> adj[V];

    // Undirected Graph Example
    adj[0] = {1, 2};
    adj[1] = {0, 3};
    adj[2] = {0, 4};
    adj[3] = {1};
    adj[4] = {2};

    vector<int> result = bfsOfGraph(V, adj);

    cout << "BFS Traversal: ";
    for (int node : result)
        cout << node << " ";
    cout << endl;

    return 0;
}

📈 Time & Space Complexity of BFS

⏱ Time Complexity → O(V + E)
V (Vertices):

• Each vertex is enqueued and dequeued at most once.
• Visiting and marking a node takes constant time → O(V). E (Edges):
• For each vertex, BFS explores its adjacency list (all connected edges).
• Across the entire graph, every edge is considered once (in undirected graphs, twice — but still O(E)).

Therefore, the total work done = O(V) + O(E) = O(V + E).

Space Complexity → O(V)

BFS requires extra memory for:

• Visited array → To track whether a node has already been explored (size = V).
• Queue → In the worst case, the queue may hold all vertices of a level at once (up to V).
• Together, this means BFS uses memory proportional to the number of vertices → O(V).

Use-Cases of BFS
1.Shortest Path in Unweighted Graphs

• BFS is the go-to algorithm when you need the minimum number of steps to move from one node to another. Example:
• In a city represented as a graph (intersections = nodes, roads = edges), BFS can find the shortest route if all roads have equal weight (like equal distance or equal travel cost).
• That’s why BFS is widely used in GPS navigation systems (when edge weights are uniform).

2.Peer-to-Peer (P2P) Networks

• In P2P systems (like BitTorrent), BFS helps in discovering nearby peers efficiently. Example:
• A node starts with a small list of peers.
• BFS can explore connections level by level to quickly discover all reachable peers in the network.
• This ensures faster file sharing and efficient resource discovery.

Comments

[Kesha Vaja]

very easy explanation , and the imagination of maze is very understandable.