Welcome back to interview prep. Today we’ll tackle a new subject to help you get ready for that big technical interview: bitwise manipulation.
First the punchline to get you motivated: what is it and why do I need to know this?
In bitwise manipulation, we’re looking at numbers not from a base-10 perspective but from a base-2 perspective. For example, the number “10” in base-10 would be expressed as “1010” in base-2.
Why is this important?
For now, I’m afraid you’ll have to take it on faith that by examining numbers in this bitwise, base-2 way, we can make subtle manipulations to those numbers which makes solving certain algorithms really easy. If we tried to use base-10 for those certain algorithms, it would be a bloody mess!
Are we Onboard re: base 2 and what a bit is?
You can skip this section if you already know about base 2 and bits, otherwise read on.
Take a regular base-10 number like 156. You know from elementary school show how to read this number since you learned about place value.
Let me make a slight alteration to the image above. Let us use a more computer science-like expression for the values of the 3 columns. Instead of “100s” we’ll call it “10 to the power of 2” or 10^2. Instead of “10s”, it’s 10 to the power of 1: 10^1. Lastly the “1s” column is 10 to the power of 0: 10^0 (Remember any number to the power of 0a power calculates to “1”
I bet you got it. So here’s a quick check. Can you figure out what “10101” in base-2 works out to be in base-10?
Right! It’s 21. Starting from the right of the number, we have 1*2^4 + 0* 2^3 + 1* 2^2 + 0* 2^1 + 1 * 2^0 = 21
Let’s Learn Some Terminology
Now that we know what base 2 is, we can start using more fancy computer science terms.
Let’s just look at at base two number: 11100
Think of each number, the 1 or the 0, occupying a separate cell in a spreadsheet. In the illustration below, I’ve given each column a letter to identify it:
The fancy word for each cell of the spreadsheet is: byte
In each cell or byte, the only two numbers we can put in them is 1 or 0.
If we put a 1 in the cell, that cell or byte is said to be set or on.
In contrast, if there is a 0 stored
in the byte, that byte is said to be clear or off.
That means in our example above, we see that columns A, B and C contain bytes that are “set” or “on”, while columns D and E contain bytes that are “clear” or “off”.*
Fun aside: the bytes are represented to us humans as the integer 1 or the integer 0. However, the computer does not “see” these symbols. Just recognizes intensity of light. This means the byte containing the “1” is seen by the computer as a brighter light. The “0” is seen by the computer as a dimmer light.
Let’s Start Manipulating Those Bits!
So finally we know enough to start making some bit-wise waves!
Let’s learn some basic operations of bits:
Bitwise NOT ( ~ )
Bitwise AND ( & )
Bitwise OR ( | )
Bitwise XOR ( ^ )
Let’s take them one at a time:
Bitwise NOT
Bitwise NOT ( ~ ) is easy. If the bit is set (1) then bitwise NOT, the tilde sign ( ~ ) clears it (turns it into 0).
If the bit is clear (0) the tilde sign ( ~ ) will clear it.
So given the base two number 11100. If we apply bitwise NOT we’ll get 00011:
~(11100) = 00011
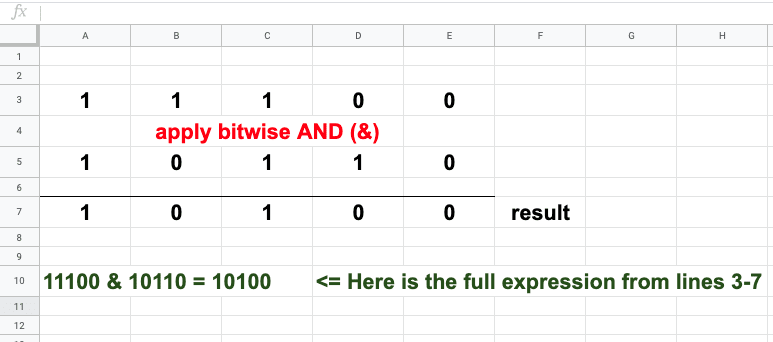
Bitwise AND
Do not confuse the regular AND symbol that you already know (&&) with BITWISE AND (&). Bitwise AND is represented by only one ampersand in the Java language. We use that bitwise AND when we’re working on the level of bits only.
Think of bitwise AND like multiplication. When we take two base-two numbers OF EQUAL LENGTH and apply bitwise AND we’ll find the result by multiplying the column of one number with the corresponding column of the second number:
Starting in column A. Multiply 1 in column 3 by 1 right below it in cell A5 and we get 1 in cell A7 as the result.
Column B: 1 x 0 gives us zero
Column C: 1 x 1 gives us 1
Column D: 0 x 1 gives us zero
Column E: 0 x 0 gives us zero
Bitwise OR ( | )
Again, notice bitwise OR is represented by only ONE pipe symbol. It is different from the normal OR ( ||) with two pipe symbols that you’re used to using in the Java language.
You can think of bitwise OR as like addition. You’ll be adding each column individually:
This time in Col A we add 1 and 1 and get technically 10 in base two, but we’ll chop of the zero and call it one.
In Col B: 0 + 1 gives us 1
In Col C: 1 + 1 gives us 1
In Col D: 1 + 1 gives us 1
In Col E 0 + 0 gives us 0
And now comes my favorite:
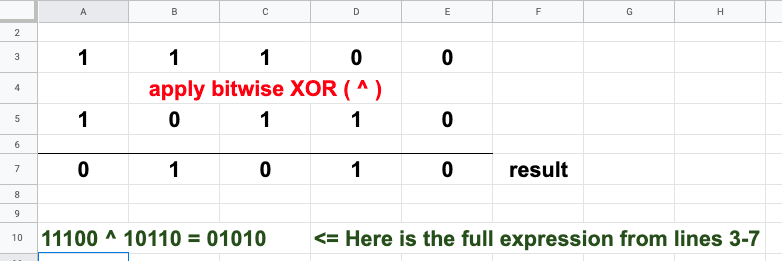
Bitwise XOR ( ^ )
XOR is pronounced EX-OR and also as ZOR (As in Zoro, the famous swordsman!)
For this one, all you have to remember is that in each column, if one number contains a “1”, the other number must contain a “0” in order to result in a “1”. If both bytes are set, or if both bytes are clear, then we’ll get “0”
Let’s see it in action:
In column A, 1 and 1 return 0
Col B: 1 and 0 return 1
Col C: 1 and 1 return 0
Col D: 1 and 0 return 1
Col E: 0 and 0 return 0
Now that you know some of the basic bit manipulations, we can begin to solve some bit manipulation algorithms which is where the beauty of bits come into play. We’ll be able to “fine tune” and make subtle distinctions between integers using base 2 and bit manipulation as opposed to using base 10 to try to accomplish the same thing. Think of the difference in your code the same as the difference between rose pedals (base 2) vs. a mess (base 10)!
See you next time for more!
And in the meantime:
Keep coding out your dreams!
Namaste!








Top comments (0)