Recently I came up with an idea for a front end side project to make a sudoku puzzle game. For that purpose, of course, I would need to get some puzzles and there are some services and API’s that could help me in this case. But I was too curious about the idea of generating puzzles by myself, so I decided to build my own sudoku generator. With this post I will share my process with you.
Strategy
In classic sudoku, the objective is to fill a 9x9 grid with digits so that each row, column and each of the nine 3x3 sections contain all digits from 1 to 9. The final puzzle is a partially completed grid (left with the clues) and for the best case scenario it should have a single solution.
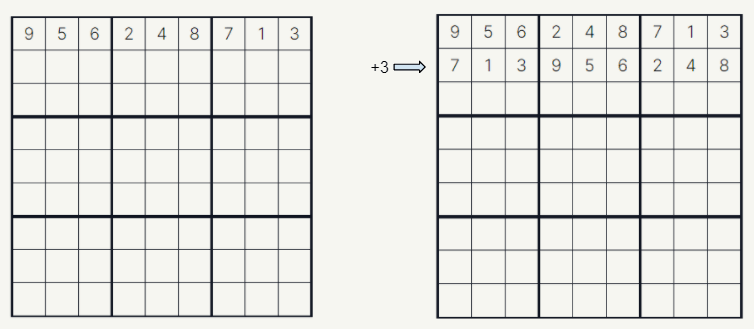
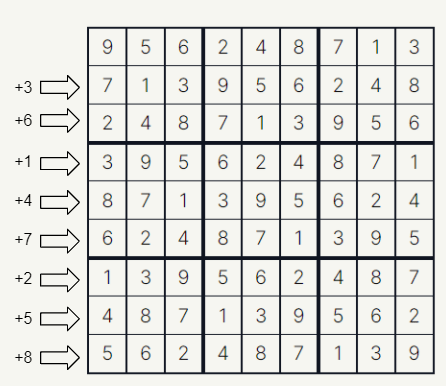
To generate a puzzle, we sure would need to get a full valid grid at first. The first thought was kind of obvious and simple: generating a row of numbers in random order, applying them to each row with a shift to one side each row. Let’s see how it looks.
Let’s try taking a random order of possible digits, f.e.: 9, 5, 6, 2, 4, 8, 7, 1 and 3.
We apply them on the first row of the grid and duplicate rows with a shift to one side by specific amount of squares.
By continuing this process we eventually end up with a valid sudoku grid.
All we need to do now is to leave out the clues. This approach is really simple and won’t require much work to apply the logic. But there is a big issue - the sudoku pattern is too obvious and the player may eventually figure it all out quite soon.
I looked for other possible approaches and I found a quite fascinating solution: run a sudoku solver on an empty sudoku grid. This approach makes the original purpose kind of more complicated, since now we would need to build both the generator and the solver.
As said earlier, once we have our valid grid, we would need to remove some numbers and leave out a certain number of clues. The difficulty of a sudoku puzzle could be determined in different ways, including the amount of clues and the amount of techniques needed for the puzzle to be solved. For the sake of simplicity of building this generator, we would only take an amount of clues to keep in mind.
Code
To represent a sudoku grid, we would use a multidimensional array grid[a][b], where a would represent a row, and b - a column. We consider a value with 0 as an empty square on the grid.
So first we need to generate an empty grid. We could hardcode it or run a nested loop 9 times each to fill up the arrays with zeros,
const generateEmptyGrid = () => {
const grid = [];
for (let i = 0; i < 9; i++) {
for (let l = 0; l < 9; l++) {
if (grid[i] === undefined) {
grid[i] = [];
}
grid[i].push(0);
}
}
return grid;
}
So an empty grid looks like this:
[
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0]
]
Next, we need to run a solver on this empty grid and for that purpose we need to build one.
For the solver I chose to use a backtrace algorithm to keep track of all of the numbers considered for each square while running through the grid.
We get the random order of numbers that will be considered by the solver.
const generateNumbersToCheck = () => {
const numbers = [1,2,3,4,5,6,7,8,9];
const numbersRearranged = [];
for (let i = 0; i < 9; i++) {
const randomIndex = Math.floor((Math.random() * numbers.length));
const [randomNumber] = numbers.splice(randomIndex, 1);
numbersRearranged.push(randomNumber);
}
return numbersRearranged;
}
This is needed because if we would use the same order to check numbers, we would end up with the same grid all over again and again.
Next we need to think about a backtrace map. Key of the map will represent the position of the grid in a format of "col,row". I put the column up first before the row because it represents the X and Y axis better this way. The values will be arrays of numbers that represent the digits that have been checked at that particular position at a particular moment.
// {[key: “col,row”]: number[]}
We get the coordinates of all the empty squares and form the map.
const getEmptySquaresList = (grid) => {
const squaresToFill = [];
for (let i = 0; i < 9; i++) {
for (let l = 0; l < 9; l++) {
if (grid[i][l] === 0) {
let squareCode = `${l},${i}`;
squaresToFill.push(squareCode);
}
}
}
return squaresToFill;
}
const getBacktraceMap = (emptySquaresList) => {
const backtraceMap = {};
const len = emptySquaresList.length;
for (let i = 0; i < len; i++) {
backtraceMap[emptySquaresList[i]] = [];
}
return backtraceMap;
}
To keep the track for the solver we will also create a pointer that will indicate which square is being checked at the moment.
- If the number can be applied to the square, we fill it in the grid and push the applied action to the backtrace map and move the pointer forward.
- If the number cannot be applied, we still need to push the action and proceed with the other following number.
- If we run out of options on the current square (array with all numbers), we move the pointer one step back, remove the applied square actions on the backtrace map and start over.
- If we end up with a negative pointer, it will mean that the grid provided to the solver was invalid. Although it is less likely to occur when running the solver on the empty grid.
Let’s put up all of this on code:
const solveSudokuPuzzle = (grid) => {
const numbersToCheck = generateNumbersToCheck();
const emptySquares = getEmptySquaresList(grid);
const backtraceMap = getBacktraceMap(emptySquares);
const pathLength = emptySquares.length;
pointerLoop:
for (let pointer = 0; pointer < pathLength; ) {
// If pointer eventually gets to -1 - puzzle is invalid
if (pointer < 0) {
throw new Error(“Error: The puzzle given is invalid”);
}
const currentSquare = emptySquares[pointer];
// Check if we have tried all of the digits on current square
if (backtraceMap[currentSquare].length === 9) {
// Reset the digits tried on current square list
backtraceMap[currentSquare] = [];
// Move pointer back
pointer--;
// Clear the previously inserted digit on the grid
const [prevCol, prevRow] = emptySquares[pointer].split(',');
insertDigit(grid, 0, prevCol, prevRow);
continue;
}
// Get the position of current square
const [col, row] = currentSquare.split(',')
singleSquareCheck:
for (let numberToGuessIndex = 0; numberToGuessIndex < 9; numberToGuessIndex++) {
const currentNumberToCheck = numbersToCheck[numberToGuessIndex];
// Check if it has not been guessed before
if (backtraceMap[currentSquare].indexOf(currentNumberToCheck) === -1) {
// Check if it can be inserted
const canBeInserted = canNumberBeInserted(grid, currentNumberToCheck, x, y);
// Append as a considered number
backtraceMap[currentSquare].push(currentNumberToCheck);
if (canBeInserted) {
// Apply number and move on
insertDigit(grid, currentNumberToCheck, x, y);
pointer++;
break singleSquareCheck;
}
}
}
}
return grid;
}
We run a loop for the pointer (pointerLoop) to go through all empty grid squares. We do a check if the pointer is negative, which would mean that the grid was invalid and throw an error in that case. We also do a check if we have tried all of the numbers for the particular square and if so, we move the pointer one step back and reset previous actions. If we are good to go, we check for possible numbers at the particular square (singleSquareCheck loop). If we find a digit that can be inserted, we apply it to the grid and move on. If we try all of the numbers, we will eventually get back to the previous check.
We also used some additional helpers over there.
insertDigit inserts a digit into a certain grid position.
const insertDigit = (grid, digit, col, row) => {
grid[row][col] = digit;
}
canNumberBeInserted checks if number doesn’t occur in grid's 3x3 section, current row and current column.
const canNumberBeInserted = (grid, numberToCheck, col, row) => {
// Check for occurence in 3x3 section)
// getSectionIndexes returns the starting indexes of needed 3x3 section
const [startingCol, startingRow] = getSectionIndexes(col,row);
for (let i = 0; i < 3; i++) {
for (let l = 0; l < 3; l++) {
const colIndexToCheck = startingCol + l;
const rowIndexToCheck = startingRow + i;
if (grid[colIndexToCheck][rowIndexToCheck] === numberToCheck) {
return false;
}
}
}
// Check for the occurence in row
for (let i = 0; i < 9; i++) {
if (grid[row][i] === numberToCheck) {
return false;
}
}
// Check for the occurence in column
for (let i = 0; i < 9; i++) {
if (grid[i][col] === numberToCheck) {
return false;
}
}
return true;
}
Now when we have a full grid we can start removing numbers.
Back to the strategy
As mentioned earlier, the number of clues would depend on the difficulty selected.
- Easy sudoku would have 36-45 clues
- Medium sudoku would have 27-35 clues
- Hard sudoku would have 19-26 clues
- Evil sudoku would have 16-18 clues
A helper for determining amount of clues could look like this.
const getNumberOfClues = (difficulty) => {
switch(difficulty) {
case 'evil':
return Math.floor(Math.random() * 2) + 16;
case 'hard':
return Math.floor(Math.random() * 7) + 19;
case 'medium':
return Math.floor(Math.random() * 9) + 27;
case 'easy':
return Math.floor(Math.random() * 9) + 36;
default:
return Math.floor(Math.random() * 27 + 16);
}
}
Now we need to remove that amount of digits on the grid. It would look simple to remove them by random order, but we should apply some pattern of removal. Why? Because if we try to generate a puzzle by removing random numbers and leaving 27 clues, we can end up with puzzles like this:
It’s a small possibility to catch edge cases like these. We could try to apply a pattern of removal to get a puzzle with a more even distribution of hints. One of the approaches I found was to pick and remove a random square and it’s opposite square that is located on the counter-side. Like this:

But then our puzzles will have a pretty obvious mirrored clues pattern:

So another thing we could do here is to shift the grid by zero, one or two thirds each direction:
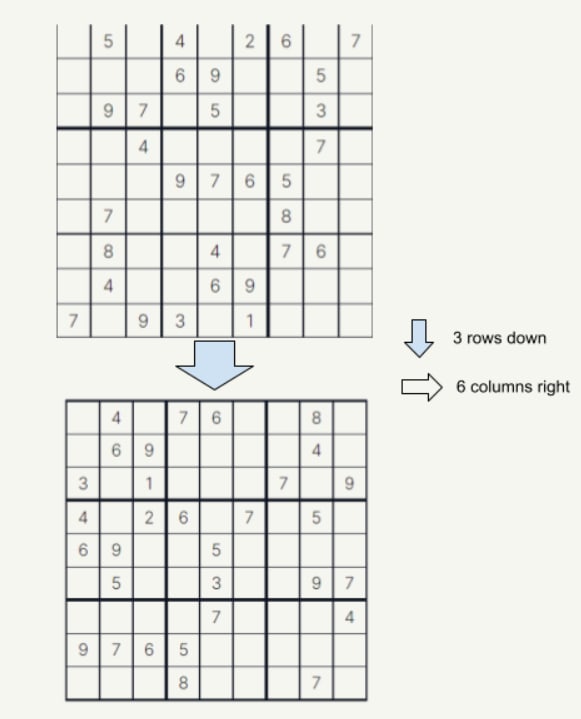
Now it looks quite solid!
Back to the code
const leaveClues = (grid, cluesCount) => {
const squaresToClearCount = 81 - cluesCount;
// Have all available square indexes in one array
const allSquareIndexes = [];
for (let i = 0; i < 9; i++) {
for (let l = 0; l < 9; l++) {
allSquareIndexes.push(`${l},${i}`);
}
}
// Get indexes of squares that are going to be cleared
const squaresToClear = [];
for (let counter = 0; i < squaresToClearCount;) {
const [randomSquare] = allSquareIndexes.splice(Math.floor(Math.random() * allSquareIndexes.length), 1);
squaresToClear.push(randomSquare);
counter++;
// We keep track of counter instead of iteration, because we may want to get multiple squares on single iteration
// If we reach the limit here, stop the loop
if (counter === squaresToClearCount) {
break;
}
// If random square is center square, it will not have a counter square
if (randomSquare === '4,4') {
continue;
}
const counterSquare = getCounterSquare(randomSquare);
const indexOfCounterSquare = allSquareIndexes.indexOf(counterSquare);
if (indexOfCounterSquare !== -1) {
allSquareIndexes.splice(indexOfCounterSquare, 1);
squaresToClear.push(counterSquare);
counter++;
}
}
// Clear those digits from the grid
for (let i = 0; i < squaresToClear.length; i++) {
const [col,row] = squaresToClear[i].split(',');
insertDigit(grid, 0, col, row);
}
// Shift the grid
shiftGrid(grid);
return grid;
}
We used some more helpers to finish the puzzle.
const getCounterSquare = (square) => {
const [col, row] = square.split(',');
const counterRow = 8 - Number(row);
const counterCol = 8 - Number(col);
return `${counterRow},${counterCol}`;
}
const shiftGrid = (grid) => {
const xThirds = Math.floor(Math.random() * 3) + 0;
const yThirds = Math.floor(Math.random() * 3) + 0;
if (xThirds === 0 && yThirds === 0) {
return;
}
// Shift rows
if (yThirds > 0) {
for (let i = 0; i < yThirds * 3; i++) {
const lastRow = grid.pop();
grid.unshift(lastRow);
};
}
// Shift columns
if (xThirds > 0) {
for (let i = 0; i < 9; i++) {
for (let l = 0; l < xThirds * 3; l++) {
const lastRowNumber = grid[i].pop();
grid[i].unshift(lastRowNumber);
}
}
}
}
With this code we still might get a mirrored clues pattern, but not all of the time.
And that is it! We can get a sudoku puzzle of desired difficulty. We can even customize code a little bit to generate a puzzle with the desired number of clues. Some of the written helpers might even be useful in the game itself.
If you reached this far, thank you for reading!




Top comments (0)