I use to write things in order to learn them so here is a series of short articles about what I didn’t know.
The Numeric Class
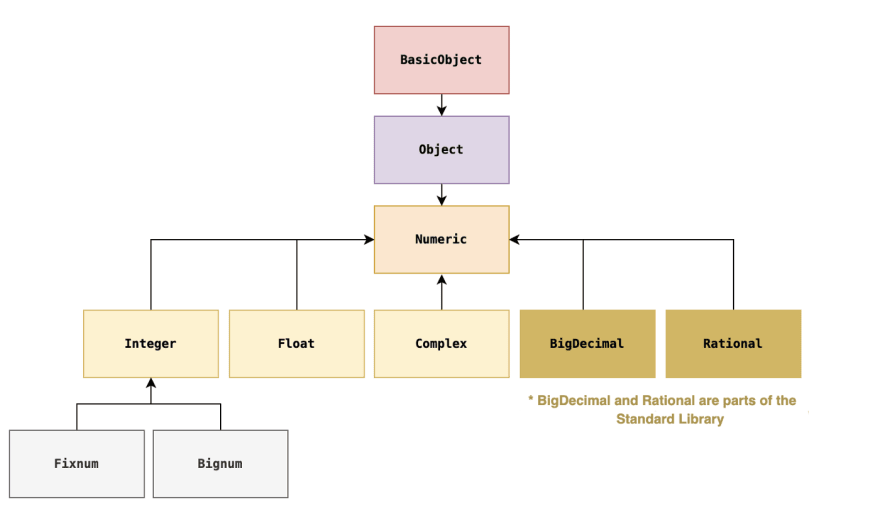
In Ruby, what we call “numbers” are all objects from the Numeric class as we can see on the following diagram :
Fixnum and Bignum
Fixnum are representing small integers and Bignum are representing big integers. As the doc says : “Holds Integer values that can be represented in a native machine word (minus 1 bit).”
Since ruby 2.4, Fixnum and Bignum are unified under the Integer class, so depending on your ruby version, you will get a different behavior.
# Before Ruby 2.4
>> 3.class
=> Fixnum
>> 30000000000000.class
=> Bignum
# After Ruby 2.4
>> 3.class
=> Integer
>> 30000000000000.class
=> Integer
Use underscores to improve your readability
You can use underscores to get more readable numbers when they reach one thousand.
>> 1_000 + 1
=> 1001
1_350_800 - 1_000_000
=> 350800
Divmod vs Modulo operators
As the doc specifies, Divmod is a method that returns an array containing the quotient and modulus obtained by dividing num by numeric., in other words :
>> 13.divmod(3)
=> [4, 1]
# The quotient 4 means that we get 4 times 3 in 13 (4 * 3 = 12) and it rests 1 (12 + 1 = 13).
Using the modulo operator (%) with positive values is pretty easy to understand as it gives you the rest of a division :
>> 13%3
=> 1
>> 13.modulo(3)
=> 1
# it is equivalent to 13.divmod(3)[1]
but using it with negative values can be really complicated. I am not going to explain it deeper here and I prefer to give you some resources that will do it far better than me :
Why is the behavior of the modulo operator (%) different between C and Ruby for negative integers?
Exploring the difference between modulus and remainder in Ruby’s Numeric class
Floats are not exact …
Every developer knows that float are decimal numbers but I didn’t know that floats were inexact real numbers.
>> 4.0 - 3.1 == 0.9
=> false
>> 4.0 - 3.1
=> 0.8999999999999999
This is due to the limited number of bytes that can store a Float, so sometimes a Float is not exactly equals to what you think… And here comes the BigDecimal class.
… but BigDecimals are
BigDecimal provides arbitrary-precision floating point decimal arithmetic. In some precise cases, you will need to use BigDecimal in order to overcome the inexactitude of floats.
>> require 'bigdecimal'
=> true
>> BigDecimal('4.0') - BigDecimal('3.1') == 0.9
=> true
Rationals
The docs says that a rational number can be represented as a pair of integer numbers: a/b (b>0), where a is the numerator and b is the denominator. In other words, rationals are similar to fractions.
>> (2/3).class
=> Integer
>> (2/3r).class
=> Rational
>> 1.5.to_r
=> (3/2)
You can run all the “+”, “ /”, “-” and “*” operations between Rationals
>> (1/8r) + (7/8r)
=> (1/1)
The last word
I know there are lots of other concepts around the Numeric class but that’s all for this article, feel free to improve my explanation in the comments, I might add more concepts here in the future 👋
Connect with me :



Top comments (0)